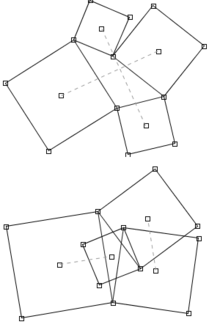
 판아우벌 정리는 사각형에도 응용할 수 있다.
판아우벌 정리는 사각형에도 응용할 수 있다.
판아우벌 정리는 네덜란드 수학자 헨리퀴스 휘베르튀스 판아우벌(Henricus Hubertus van Aubel)의 이름이 붙은 정리이다.
공식화[편집]
 판아우벌 정리
판아우벌 정리
삼각형 ABC (△ABC)의 각 꼭짓점에서 삼각형 ABC 내부의 임의의 한 점 P와 만나는 세개의 직선 AP, BP, CP가 각각 선분 BC, CA, AB와 만나는 점을  ,
,  ,
,  이라고 할 때 (
이라고 할 때 ( ,
,  ,
,  )
)
다음과 같은 식이 성립하는데,

이를 판아우벌 정리라고 한다.
증명 Ⅰ[편집]
 는 삼각형
는 삼각형  의 면적을 뜻한다.
의 면적을 뜻한다.
삼각형  와 삼각형
와 삼각형  는 동일한 선분
는 동일한 선분  를 밑변으로 가지고 있으므로 높이(선분)의 비율은 면적의 비율과 동일하다. 따라서
를 밑변으로 가지고 있으므로 높이(선분)의 비율은 면적의 비율과 동일하다. 따라서
 가 성립하는데
가 성립하는데
이것은
 을 내포한다.
을 내포한다.
또 삼각형  과 삼각형
과 삼각형  을 보면 두 삼각형은 동일한 선분
을 보면 두 삼각형은 동일한 선분  을 같은 높이로 가지고 있으므로 밑변(선분)의 비율은 면적의 비율과 동일하다. 따라서
을 같은 높이로 가지고 있으므로 밑변(선분)의 비율은 면적의 비율과 동일하다. 따라서
 가 성립한다.
가 성립한다.
위와 동일한 방법으로
 을 얻을 수 있다.
을 얻을 수 있다.
따라서

위 식을 정리하면,
- (i)

이와 같은 방법으로 동일하게 구하면
- (ii)

(i)식과 (ii)식을 각각 더하면

판아우벌 정리를 증명할 수 있다.
증명 Ⅱ[편집]
판아우벌 정리는 메넬라오스 정리와 체바 정리를 이용하여 증명할 수 있다.
삼각형  과 직선
과 직선  에 대해서 메넬라오스 정리가 성립한다.
에 대해서 메넬라오스 정리가 성립한다.

이 식을 변형하면,

따라서,
- (i)

삼각형  에서 체바 정리가 성립한다.
에서 체바 정리가 성립한다.

따라서,
- (ii)

(ii)식을 (i)식에 대입하면

증명 Ⅲ[편집]
 | 이 문단은 아직 미완성입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. |
판아우벌 정리는 삼각함수를 이용하여 증명할 수 있다.[1]
같이 보기[편집]
외부 링크[편집]
































