톱니바퀴

톱니바퀴 또는 기어(gear, 문화어: 기야)는 톱니의 맞물리는 힘으로 동력을 전달하는 장치이다. 간단한 단순 기계다.
2축의 회전 방향이 서로 반대이면, 벨트전동에서는 십자걸기(十字掛)로 하면 좋으나 벨트를 사용치 않고, 벨트바퀴와 동일한 원형바퀴(圓形車)를 직접 접촉시켜서 구름 마찰에 의해서 동력을 전달할 수도 있다. 구조는 간단하지만, 다음과 같은 결점이 있다.
- 미끄럼이 일어나기 일쑤이며 확실한 전동을 얻기 어려운 것,
- 큰 동력을 전하는 데는 미는 힘을 크게 해야 하므로 축받이(軸受)에 무리가 가해진다. 그래서 큰 동력을 전하는 데는 부적당하다.
이런 결점을 피하기 위해 원형바퀴의 둘레에 적당한 형상의 철기(凸起) (이빨)를 동일 간격으로 마련하고, 한쪽 바퀴의 톱니가 상대 바퀴의 이빨 사이의 홈에 순차적으로 들어감으로써, 원동바퀴(原動車)의 치면(齒面)이 종동바퀴(從動車)의 치면을 밀게 되어서 동력이 전해지도록 한 톱니바퀴가 쓰인다. 회전비가 일정한 전동을 정확하게 행하게 할 수 있는 이의 형태는 여러 가지가 있지만, 현재 쓰이고 있는 것은 거의 모두 인벌류트 곡선이라 불리는 것이다.

이것은 원(圓)에 실을 감았다가 풀어 갈 때, 실 끝에 단 펜이 그리는 곡선이다. 이 곡선이 치형으로 사용될 수 있는지 알아보자. 십자걸기벨트바퀴를 생각해 보자. 벨트 위의 한점 C에 장치한 펜이, 각 벨트바퀴에 고정해서 함께 회전하는 지면 위에 그리는 곡선을 생각하면, 벨트바퀴는 원, 벨트는 실에 상당하므로 이 곡선은 인벌류트곡선인 것이며, 실은 곡선의 법선이다. 따라서 이 곡선을 각 바퀴의 치형으로 하면 벨트에 상당하는 직선 위에서의 맞물림이 행해지며, 벨트에 의한 회전운동과 동일한 운동을 얻게 된다. 반대방향의 회전도 전해지도록, 대칭인 인벌류트곡선으로 톱니의 양면을 형성하고, 이것을 벨트바퀴 둘레 위에 동일 간격으로 배치함으로써 서로 맞무는 한쌍의 톱니의 맞물림이 끝나기 전에 다음의 한쌍의 톱니가 맞무는 것을 시작하도록 하면 연속적으로 회전을 전할 수가 있다. 벨트가 양톱니바퀴의 중심을 맺는 직선(중심선)과 교차되는 점은 톱니바퀴 중심 사이를 회전비의 역비로 내분하는 점이며, 이 톱니바퀴와 동일한 운동을 전하는 굴림마찰바퀴의 접촉점으로 된다. 이 점을 피치점이라 한다. 이 굴림마찰바퀴의 윤곽원(輪廓圓)을 피치원, 벨트바퀴의 원을 기초원(基礎圓)이라 한다. 피치원에 좇아서 측정한 것의 간격을 원피치라 한다.
원피치(단위는 mm)를 원주율 π로 나눈 값(値)을 모듈이라 하고, 이의 크기를 나타내는 기준량으로서 사용한다. 모듈에 이빨의 수를 곱한 것이 피치원의 직경에 맞먹는다. 또 피치원에서 톱니 끝에 걸쳐서의 높이는 보통 모듈과 동등하게 한다. 인벌류트 톱니바퀴에서는 벨트전동과 동일하게 중심 사이의 거리리가 변할지라도 회전비에 변화가 없다는 이익점(利益點)이 있다.
톱니바퀴의 역학[편집]
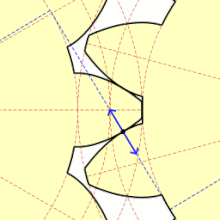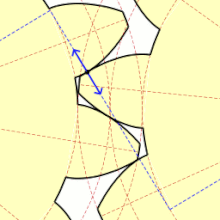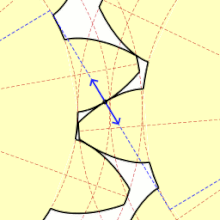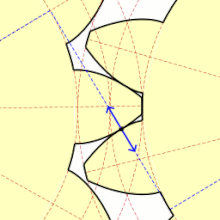
맞무는 점에서 톱니면의 법선 방향으로 작용하는 힘(法線荷重)은 항상 피치점으로 향하는 방향으로 일하고, 그 작용선은 인벌류트 톱니바퀴에서는 기초원의 공통접선(가상벨트)과 일치한다. 피치점 이외의 맞물림점에서는 치면이 상대적으로 미끄러지면 접촉하므로 치면의 공통 접선 방향으로 마찰력이 작용하지만, 그 크기는 대략 법선 하중의 1/10 정도이다. 이 마찰력의 방향은 치면의 서로 마찰되는 방향에 따라서 정해지며, 맞물림의 시점(始點)으로부터 피치점에 접근하는 동안 종동바퀴(從動車)의 회전을 방해하고, 피치점에서부터 멀어지는 동안은 회전을 돕도록 작용한다. 따라서 맞물림점의 이동에 따라서 힘의 크기가 다소 변화하고, 또 맞물림의 쌍수가 2쌍 이상이 되면 각 맞물림점에 하중이 배분된다.
톱니는 하중에 의해서 부러지지 않도록 십분 튼튼하게 만듦과 동시에 치면이 빨리 닳아지지 않도록, 맞물림점에 생기는 응력(접촉응력)이 너무 커지지 않도록 설계하여야 한다. 마찰력을 생략하고 생각하면, 법선하중과 같은 크기의 하중이 축받이에 작용한다. 법선하중의 작용선이 중심선과 이루는 각의 여각(餘角) α를 압력각이라 한다. 그것은 전달토크 Ti(i=1,2)를 일정하다고 하고, 피치원 반경을 Ri로 하면, 법선하중 FN은,
- FN = Ti / RiCosα (RiCosα = 기초원 반경)
로 나타내지며, 압력각 α가 클수록 축받이 압력이 커지기 때문이다. 압력각의 크기는 대략 14.5° ~ 30°의 범위를 취한다.
이끊기법과 전위치차[편집]
톱니바퀴의 톱니는 주조로 만드는 수도 있지만, 흔히는 인물(刃物)로 톱니홈(齒溝) 부분을 깎아서 만든다. 톱니수의 많고 적음에 관계없이, 피치원 위의 톱니의 두께가 피치의 절반이며 톱니의 높이가 양바퀴에 있어 서로 동등한 표준 톱니바퀴에서는, 톱니수가 적을 때는 톱니의 뿌리 밑에 가까운 곳이 날끝으로 패어 나가 톱니가 약해지고, 맞물림성도 좋지 않으므로, 절하(切下)라고 해서 날도구를 알맞게 후퇴시켜서(이것을 정의 전위라 한다) 톱니를 깎아 내는 수가 많다. 이렇게 하면 톱니는 밑뿌리가 굵어지고, 인벌류트의 기초원으로부터 떨어진 부분을 이용하므로, 강도라든가 맞물림 성능이 좋아진다. 톱니수가 많은 톱니바퀴는 날을 전진시켜서(이것을 부의 전위라 한다) 톱니를 자르는 수도 있다. 이리하여 톱니를 깎은 것은 올바르게 맞물지만, 중심거리나 맞물림 압력각은 표준적인 것과는 달라진다. 이를 전위톱니바퀴라고 한다. 단 작은 톱니바퀴를 정전위(正轉位)하고 큰 톱니바퀴를 같은 양만 부(負)전위하면, 중심거리도 맞물림 압력각도 표준 톱니바퀴와 동일하게 되지만, 치말(齒末)의 높이는 양바퀴가 서로 동등하지 않다. 전위량을 적정(適正)하게 선택하면, 톱니의 세기나 성능을 현저히 개선시킬 수 있으므로, 현재의 톱니바퀴는 대부분 전위톱니바퀴로 되어 있다.
여러 가지 톱니바퀴[편집]

톱니바퀴는 회전을 전하는 2축의 상대적 위치에 따라서 평행축톱니바퀴·교차축톱니바퀴·엇물림축톱니바퀴의 3종으로 크게 나뉘며, 다시금 치형(齒形)의 구성 방식에 따라서 여러 종류가 있는데, 그 중의 주요한 것을 〔그림〕-25로 표시한다. 평행축톱니바퀴는 굴림접촉원통면(圓筒面)을 톱니를 마련하는 기준면(피치면)으로 한다. 평(平)톱니바퀴(a)는 가장 보편적으로 쓰이는 기본적인 톱니바퀴이며, 앞에서 말한 치형(齒形)의 설명은 이 평톱니바퀴의 축직각단면(軸直角斷面)에 대해서 말한 것이다.

경삿니톱니바퀴(b)는 피치원통 위의 덩굴 감기선에 따른 비틀어진 톱니를 갖는 것으로 맞물림이 원활하게 행해지며 고속도로 큰 동력을 전할 수가 있지만 축방향으로 서로 미는 힘(스러스트)이 생기므로, 이것을 받는 스러스트축받이가 필요하게 된다. 산형(山形)톱니바퀴(c)는 비틀림이 반대인 경삿니톱니바퀴를 짜맞추어서 스러스트가 서로 지워지도록 한 것이다. 안톱니바퀴(內齒車) (d)는 회전방향이 동일하며, 안쪽에 작은 톱니바퀴가 있다. 작은 톱니바퀴와 래크(e)는 직선운동과 회전운동의 변환에 쓰이는데, 인벌류트 톱니바퀴의 래크의 치형은 간단한 직선으로 되므로, 톱니를 공작하는 데 편리하다.
교차축(交叉軸)톱니바퀴 중 우산톱니바퀴는, 2축의 교차점을 정점(頂點)으로 하는 굴림접촉원추면을 피치면으로 한 톱니바퀴로서, 곧은니톱니바퀴(f)가 가장 많이 쓰인다. 고속고마력(高速高馬力)인 경우는, 굽은니양산톱니바퀴(g)가 쓰인다. 빗물기축톱니바퀴는 여러 종류가 있는데 나사톱니바퀴(i)는 경삿니톱니바퀴를 축을 빗물게 해서 맞물린 것으로, 맞물림이 톱니면 위의 한 점에서 행해지므로 큰 동력의 전달에는 알맞지 않다. 직각 또는 직각에 가까운 2축 사이에 고감속비(高減速比)로 회전을 전하는 데는 웜기어가 쓰인다. 원통 모양의 나사를 작은 톱니바퀴(웜)로 하는 원통 웜기엄(j)가 보통이다. 강(強)부하인 경우는, 고형(鼓形) 웜기어(k)가 쓰인다.

굽은니우산톱니바퀴를 닮은 하이포이드기어는 자동차의 후차축의 구동(驅動)에 많이 쓰인다. 축이 직각 또는 이에 가까운 각을 이루고 교차되거나 엇갈려 있는 경우에, 작은 톱니바퀴로서 평톱니바퀴 또는 경삿니톱니바퀴를 사용한 페이스이거(h)를 사용하는 수도 있다. 각속비(角速比)가 변동하는 톱니바퀴에는 비(非)원통톱니바퀴(m)라든가 편심(偏心)톱니바퀴(n) 등이 있다.
톱니바퀴의 조합[편집]
원동축(原動軸)과 종동축(從動軸) 사이의 톱니바퀴를 여러 모양으로 짜맞춤으로써 필요로 하는 운동을 전달할 수가 있다. 이것을 톱니바퀴열(列)이라 한다. 그림〕-26과 같이 톱니바퀴축을 고정지지(固定支持)틀로 지탱하며 몇 개의 톱니바퀴(이 그림에서는 6개)를 계속해서 맞물게 했을 경우, 톱니바퀴의 톱니수를, 그 회전속도를 로 나타내면, 톱니바퀴비로 나타내게 된다. 〔그림〕-27과 같이 중간톱니바퀴(2, 3바퀴)를 사용한 경우는 위 식으로 놓은 경우에 상당하며, 로 되고 중간톱니바퀴의 톱니수는 톱니바퀴비(比)와는 무관하게 되지만, 톱니바퀴의 개수가 기수냐 우수냐에 따라서 종동축(從動軸)의 회전방향이 원동축과 동일하거나 반대가 된다.
톱니바퀴 변속장치[편집]
톱니바퀴의 짜맞춤의 변화에 따라서, 원동축의 일정한 회전속도에 대하여 종동축의 회전속도를 몇 가지 범위로 변환하는 장치를 톱니바퀴변속장치라고 말하고, 종동축의 회전속도가 만드는 수열을 속도 열이라 한다. 공작기계나 자동차 등에는 등비수열이 쓰이는 수가 많은데, 계산기 등에는 등차수열도 사용된다. 속도변환의 방법에는 여러 가지가 있다.
바꿈톱니바퀴[편집]
톱니바퀴를 떼내고 딴 것으로 바꿔 끼우는 방식으로, 번번이 딴 것과 바꿀 필요가 없는 자동기(自動機) 등에 사용된다.
클러치에 의한 변속[편집]
각(各) 톱니바퀴 쌍(雙)을 항상 맞물려 한쪽의 축 위에서 헛돌게 해 놓고, 그 축과 함께 회전하는 클러치를 다른 어떤 톱니바퀴와 결합시켜서 전동(傳動)을 행하게 하는 방식이다. 회전중에 속도를 바꿀 경우, 부드럽게 절환이 행해지게끔 하기 위하여 원추(圓錐)마찰클러치를 작동시킴으로써, 이로부터 결합시키려고 하는 톱니바퀴를 동기속도(同期速度)로 한 후, 톱니바퀴형 클러치를 맞물림으로써 조용하고 확실하게 전동하도록 한 싱크로메시(동기맞물림)방식이 자동차라든지 공작기계에 쓰이고 있다.
미끄럼톱니바퀴에 의한 변속[편집]
한 축(軸) 위의 몇개의 톱니바퀴를 1개씩 혹은 2 ~ 3개씩 짜맞춘 것을, 스플라인 또는 미끄럼키로 축에 갖다 닮으로써 회전을 전하도록 하고, 이것을 축방향으로 미끄러뜨림으로써 상대톱니바퀴와 선택적으로 서로 맞물게 하는 방법이다.
텀블러기어(노르톤기어)[편집]
tumbler gear(norton gear) 몇 개의 톱니바퀴를 한 축 위에 톱니바퀴수의 순서로 늘어놓아 축에 고정시키고, 다른 축 위에 1개의 미끄럼톱니바퀴와 중간톱니바퀴를 갖다 단 링크를 미끄러뜨림으로써, 선택적으로 맞물게 하는 방법이다.
각종 짜맞추기[편집]
여러 종류의 속도를 얻고 싶을 때에, 위에 말한 여러 방법을 적절히 짜맞추어서 사용하는 수가 있다.〔그림〕-24는 미끄럼톱니바퀴와 클러치를 짜맞추어서, 3쌍의 톱니바퀴로 4종류의 속도를 얻는 방법을 보였다. 맞물림은 a→a′, b→b′, c-c′ 및 a→a′=b→b′=c→c′의 4종으로 I축에서부터 IV축에 회전을 전하는데, 앞의 3개의 치수비(齒數比)를 a/a′=Aφ, b/b′=A, c/c′=Aφ2로 하면, 최후의 맞물림톱니바퀴수는 Aφ×(1/A)×Aφ2=Aφ3로 되어서, 4종류의 속도가 등비급수를 이루므로 형편이 좋다.

유성톱니바퀴[편집]
톱니바퀴 장치 중의 변종은 유성톱니바퀴 장치일 것이다. 이것은 고정된 톱니바퀴 또는 고정중심 둘레를 회전하는 톱니바퀴(이것들을 태양톱니바퀴라 한다)와, 그것과 맞물고 그 둘레에서 공전하는 중심상에서 회전하는 톱니바퀴(이것을 유성톱니바퀴라 함)로써 이뤄지는 톱니바퀴 장치로서, 여러 가지 형태의 것이 있다. 그림〕-28은 그 일례로 팔E가 회전하여, 고정태양톱니바퀴 A로부터 유성톱니바퀴 B 및 C(C는 B와 함께 돈다)를 거쳐, 고정태양톱니바퀴 A와 동심(同心)인 회전태양톱니바퀴 D로 되돌려서 회전을 전한다.
각속도의 관계를 구하기 위해서는 우선 팔 E를 고정했다고 가정하고서 톱니바퀴 A의 회전에 대한 각 톱니바퀴의 회전을 생각하고, 다음에 톱니바퀴 A와 함께 전체에 회전을 부여하는 것으로 하고 각 톱니바퀴의 회전을 생각하면〔표〕-3과 같이 된다.
따라서 태양톱니바퀴 D의 회전속도는 로 된다. 이 관계에서 라면 D와 E는 동방향(同方向) 회전, 라면 역방향회전, 라면 D는 회전하지 않고, ac≒bd일 때는 로 되어서 현저한 감속을 얻게 된다. 행성톱니바퀴 장치에는 태양톱니바퀴로서 안톱니바퀴(內齒車)를 사용한 것이라든지, 톱니바퀴기구(機構) 전체를 우산톱니바퀴로 구성한 것 등도 있다.
행성톱니바퀴 장치에서 어느 톱니바퀴도 고정하지 않고 2개의 톱니바퀴에 원운동을 부여하면, 나머지 톱니바퀴의 운동은 전부 결정되며, 이 같은 운동은 1차식 형태로 결부시킨 것 같은 것이 된다. 이 같은 톱니바퀴 장치를 차동(差動)톱니바퀴 장치라고 한다.
그림〕-28의 기구에서 톱니바퀴 A에는 회전을 부여했다고 하면, 우선 E를 고정시킨 것으로 가정하고서 각 톱니바퀴의 회전속도를 구하고, E에 회전를 부여하는 것으로 하고서 각 톱니바퀴의 속도를 구하면 〔표〕-5와 같이 된다. 따라서 다음 식이 얻어진다.
태양톱니바퀴로서 안톱니바퀴를 이용한 것도 있으며 장치가 작아진다는 이익점이 있다.
우산톱니바퀴를 이용한 차동톱니바퀴기구는 자동차나 공작기계 등에 쓰이고 있다. 가장 널리 이용되고 있는 것은 〔그림〕-31과 같은 것이다. A와 D는 같은 톱니수의 우산톱니바퀴로서 이들에게 공통으로 맞물고 있는 우산톱니바퀴 B와, B를 보지(保持)하고 있는 축 C가 회전속도 로 회전하고 있을 때, A 및 D의 회전속도 와의 사이의 관계는 〔표〕-4와 같이 되며, 로 된다. 〔그림〕-29는 이 기구를 자동차의 후차축의 구동에 응용한 경우를 표시하며, 커브를 삥 돌아갈 때 위에 기록한 관계에서 안쪽 차축의 회전이 준 분만큼 바깥쪽 차축의 회전이 늘며, 슬립을 일으키지 않고 매끈하게 커브를 돌 수가 있게 된다.
참고로 우리말로 번역할 때 유성기어(톱니바퀴)로 번역되어 대부분 유성기어로 알고 있으나 행성기어,행성톱니바퀴로 바꾸어야 되는 용어임 (원어: planetary gear)
같이 보기[편집]
참고 문헌[편집]
외부 링크[편집]
 위키미디어 공용에 톱니바퀴 관련 미디어 분류가 있습니다.
위키미디어 공용에 톱니바퀴 관련 미디어 분류가 있습니다.
