자체 에너지

물리학에서 자체 에너지(영어: Self-energy)는 입자가 자신 및 주변이 만들어내는 영향으로 얻게 되는 에너지를 뜻한다.

양자장론에서 자체 에너지는 장(field)으로 표현되는 기본 입자가 자신의 장 및 주변이 만들어내는 장과의 상호 작용으로 발생하는 에너지 또는 유효 질량이 생성되는 과정에서 일어나는 기여도를 뜻한다. 여기서 '자체(self)'라는 용어는 입자가 가상 입자와의 교환을 통해 자기 스스로와 상호 작용하는 것을 뜻하며, 자기 자신 및 다른 입자 및 주위의 장에서 비롯되는 모든 상호 작용을 포함한다. 정전기학에서 전하 분포를 구성하는 데 필요한 자체 에너지란 전기력이 0이 되는 무한대로부터 전하들을 가져와서 해당 전하 분포를 만들어내는 데 필요한 모든 에너지를 뜻한다. 응집물질물리학에서의 자체 에너지는 전자가 주변 매질과의 상호 작용으로 느끼는 퍼텐셜을 나타낸다. 화학에서 이온의 자체 에너지는 이온이 스스로 만들어내는 장을 통해 얻는 에너지를 뜻한다.

양자장론에서의 설명[편집]

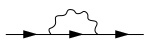
양자장론에서 자체 에너지는 운동량-에너지 표현에서 적절한 자체 에너지 연산자 (또는 적절한 질량 연산자 )의 질량껍질 값과 같다(더 정확하게는 해당 값에 $\hbar$ 를 곱한 것이다). 이를 파인만 도형을 통해 나타내면 아래의 그림과 같다.

여기서 세 개의 화살표가 있는 직선은 전파 인파를 나타내며, 물결선은 입자-입자 상호 작용을 나타낸다. 이때 가장 왼쪽과 가장 오른쪽에 있는 직선을 절단하고 나머지만 취하면 자체 에너지 연산자 자체에 대한 기여를 얻는다.

일반적으로 운동량-에너지 표현에서 자체 에너지 연산자의 질량 껍질 값은 복소수 형태로 나타난다. 이때 물리적인 자체 에너지는 실수 부분에 해당하며, 허수 부분의 역은 입자의 수명에 대한 척도가 된다.

자체 에너지 연산자 $\Sigma _{}^{}$ 는 기본 전파 인자 $G_{0}^{}$ 및 실제 전파 인자 $G_{}^{}$ 를 가지고

G=G_{0}^{}+G_{0}\Sigma G.

와 같이 나타낼 수 있다. 이를 다이슨 방정식이라고 한다. 여기서 연산자의 왼쪽에 $G_{0}^{-1}$ , 오른쪽에 $G^{-1}$ 을 취하면 다음

\Sigma =G_{0}^{-1}-G^{-1}

을 얻는다. 자체 에너지 연산자 $\Sigma _{}^{}$ 에 대한 전개를 파인만 도형으로 나타내면 다음과 같다:

양자색역학에서 워드-다카하시 항등식이 말해주는 한 가지 결과는 광자 및 글루온은 게이지 대칭성이 질량을 얻지 못하게 하므로 재규격화를 통해 질량을 얻지 못한다는 것이다. 반면 W 및 Z 보손은 힉스 메커니즘을 통해 질량을 얻는데, 이때 전자기약력의 재규격화를 통해 질량을 얻게 된다.

내부 양자수를 갖는 중성 입자는 가상 입자 쌍의 생성을 통해 서로 섞일 수 있다. 이러한 현상의 한 가지 예는 중성 케이 중간자의 섞임이다.

참조[편집]

A. L. Fetter, and J. D. Walecka, Quantum Theory of Many-Particle Systems (McGraw-Hill, New York, 1971); (Dover, New York, 2003)
J. W. Negele, and H. Orland, Quantum Many-Particle Systems (Westview Press, Boulder, 1998)
A. A. Abrikosov, L. P. Gorkov and I. E. Dzyaloshinski (1963): Methods of Quantum Field Theory in Statistical Physics Englewood Cliffs: Prentice-Hall.
Alexei M. Tsvelik (2007). 《Quantum Field Theory in Condensed Matter Physics》 2판. Cambridge University Press. ISBN 978-0-521-52980-8.
A. N. Vasil'ev The Field Theoretic Renormalization Group in Critical Behavior Theory and Stochastic Dynamics (Routledge Chapman & Hall 2004); ISBN 0-415-31002-4; ISBN 978-0-415-31002-4
John E. Inglesfield (2015). 《The Embedding Method for Electronic Structure》. IOP Publishing. ISBN 978-0-7503-1042-0.