에어리 원반

에어리 원반(Airy disk)이란 광학에서 원형의 구경을 통과한 점광이 빛의 회절 한계까지 만들 수 있는 최적의 상을 말한다.
원형 구경(사진기, 망원경 등)을 통과한 빛은 회절되어 중심에 밝은 부분을 만드는데 이를 에어리 원반이라 하고, 그 주위로 밝고 어두운 고리가 교대로 나타나는 것을 에어리 무늬(Airy pattern)라고 한다. 둘 다 조지 비델 에어리의 이름이 붙은 것이다. 이 현상 자체는 에어리 이전에 존 허셜이 먼저 발견했지만, 에어리가 1835년에 처음으로 완전한 이론적 설명을 제시하였다.[1]
이 개념의 가장 중요한 응용은 카메라와 망원경이다. 이러한 렌즈로 생성 된 이미지의 해상도에는 제한이 있다. 해상도가 더 이상 렌즈의 결함에 의해 제한되지 않고 회절에 의해서만 제한되는 광학 시스템은 회절 제한 이라고한다.회절 때문에 아무리 완벽한 환경에서 아무리 완벽한 렌즈를 사용해도 사진기 또는 망원경에 맺힌 상은 에어리 원반 이상으로 분해될 수 없다. 이를 회절한계라고 한다. 에어리 원반은 물리학, 광학, 천문학에서 중요하다.
크기[편집]
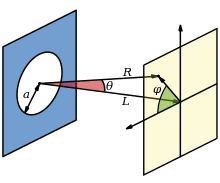
구경에서 멀리 떨어진 곳에서, 첫 번째 어두운 무늬가 나타나는 각도는 빛이 들어오는 방향에서 측정했을 때 다음과 같이 표현된다.
각도가 충분히 작을 경우에는
라고만 해도 된다. 이때 θ의 단위는 라디안이고, λ는 빛의 파장, d는 구경의 직경이다. 에어리는 이것을 다음과 같이 썼는데,
이때 s는 첫 번째 어두운 무늬가 나타나는 각도(단위: 초), a는 구경의 반경(단위: 인치), 그리고 빛의 파장은 0.000022 인치(가시광선 파장의 평균)가 사용되었다.[2]
수학적 상세[편집]
원형 구경에서 발생하는 프라운호퍼 회절 무늬(에어리 무늬)의 세기는 원형 개구의 푸리에 변환의 제곱 계수로 주어진다.
이때 는 에어리 원반 중심의 최대 세기, 는 베셀 함수, 는 파수, 는 구경의 반경, 는 관찰 각도이다. i.e. 원형 구경의 축과 구경 중심과 관찰 지점을 이은 직선이 이루는 각도 로 나타낼 수 있다. 이때 q는 관찰평면(또는 초점평면)상에서 광학축에서 떨어진 방사상 거리이고 R은 관찰 거리이다.
구경 뒤에 렌즈가 붙어 있을 경우 렌즈의 초점평면 상에 에어리 무늬가 나타난다.
가 0이 되려면 . 여기서 회절무늬에서 첫 번째 어두운 무늬는 또는
에서 나타남을 알 수 있다.
첫 번째 어두운 무늬의 반지름 은 및 개구수에 다음과 같이 유관하다.
이때 R은 구경에서의 거리, 개구수 A = sinθ은 그 거리와 구경의 크기의 비율이다. 중앙의 에어리 원반의 반높이()는 에서 나타난다.
회절무늬 중앙에서의 세기 는[3]
이때 은 구경에서 단위면적에 대한 광원 세기이고, A는 구경의 넓이(), R은 구경에서의 거리이다. 렌즈의 초점평면상에서 이다. 첫 번째 밝은 고리의 세기는 중앙의 에어리 원반의 1.75% 정도이다.
상기에 표현된 식을 합치면 어느 고리 안에 포함된 회절무늬의 총 일률을 구할 수 있다.
이때 와 은 베셀 함수이다. 이에 따라 첫 번째, 두 번째, 세 번째 어두운 고리(where ) 안에 포함되는 회절무늬의 일률은 각각 83.8%, 91.0%, and 93.8%이다.[4]
 |
 |
관찰 조건[편집]
균일하게 조명 된 원형 조리개 (또는 균일 한 평평한 빔)로부터의 광은 프라운호퍼 ( Fraunhofer) 회절 (원거리 회절)으로 인해 개구로부터 멀리 떨어진 에어리 회절 패턴을 나타낼 것이다.
원거리 장에 있고 Airy 패턴을 나타내는 조건은 다음과 같다. 조리개를 비추는 들어오는 빛은 평면파 (조리개를 가로 질러 위상 변화가 없음), 조리개 영역에 걸쳐 강도가 일정하다. R회절 된 광이 관찰되는 개구 (스크린 거리)가 개구 크기에 비해 크고, 반경 조리개는 빛의파장 λ보다 크지 않다. 마지막 두 조건은 공식적으로 다음과 같이 쓸 수 있다. R>(a^(2))/λ
실제로, 조명 원을 개구로부터 멀리 배치함으로써 균일 한 조명 조건을 충족시킬 수 있다. 원거리 장 조건이 충족되지 않은 경우 (예 : 조리개가 큰 경우) 조리개 바로 뒤의 렌즈 (또는 렌즈)를 사용하여 원거리 에어리 회절 패턴을 스크린에서 조리개에 훨씬 더 가깝게 얻을 수 있으며, 그 자체가 조리개를 형성 할 수 있다. Airy 패턴은 무한대가 아닌 렌즈의 초점에 형성된다.
따라서, 렌즈에 의해 집속 된 균일 한 원형 레이저 빔 (윗 면이 평평한 빛)의 초점은 또한 에어리 패턴 일 것이다.
카메라 또는 이미징 시스템에서, 멀리 떨어진 물체는 대물 렌즈에 의해 필름 또는 검출기 평면 상에 이미징되고, 원거리 회절 패턴은 검출기에서 관찰된다. 그 결과 이미지는 조리개 구멍으로부터의 회절 또는 렌즈의 유한한 크기로 인해 에어리 회절 패턴을 갖는 이상적인 이미지의 합성 곱이다. 이것은 위에서 설명한 렌즈 시스템의 유한한 해상도로 이어진다.
각주[편집]
- ↑ Airy, G. B., "On the Diffraction of an Object-glass with Circular Aperture," Transactions of the Cambridge Philosophical Society, Vol. 5, 1835, p. 283-291.
- ↑ Airy, G. B., "On the Diffraction of an Object-glass with Circular Aperture," Transactions of the Cambridge Philosophical Society, Vol. 5, 1835, p. 287.
- ↑ E. Hecht, Optics, Addison Wesley (2001)
- ↑ M. Born and E. Wolf, Principles of Optics (Pergamon Press, New York, 1965)

























![{\displaystyle P(\theta )=P_{0}[1-J_{0}^{2}(ka\sin \theta )-J_{1}^{2}(ka\sin \theta )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43e77cf6912164bcf59ec7e82c503a752d59df73)

