노노그램

노노그램(영어: Nonogram, 일본어: お絵かきロジック 오에가키로짓쿠[*])은 일본의 퍼즐 게임이다.[1] 각각 적혀있는 숫자를 보면서 숨겨져 있는 숫자를 예상하여 지워나가면서 그림을 그리는 게임이다. NP-완전 문제이다. 한국에서는 네모네모로직이라고 불린다.
기본적인 규칙[편집]
숫자가 하나인 경우[편집]
1개의 숫자는 연속해서 검게 칠하는 칸(이하 ‘검은 칸’)의 수를 나타내고 있다. 단, 위치까지 나타내고 있는 것은 아니다.
(예시
| 3 |
에 대해서는 다음의 3개의 가능성을 생각할 수 있다.
| 3 | |||||
| 3 | |||||
| 3 |
숫자가 여러개인 경우[편집]
‘빈칸’에 대해서[편집]
숫자가 둘 이상인 경우에 각각이 검은 칸의 수를 나타내며
사이에는 반드시 검게 칠하지 않은 칸(이하 ‘빈칸’)이 최소 하나가 들어간다.
단, 하얀 칸의 위치와, 검은 칸 사이에 얼마나 들어갈 지는 나타내고 있지 않다.
(예시1)
| 1 | 1 |
에 대해서는 여섯 가지의 방법을 생각할 수 있다.
| 1 | 1 | |||||
| 1 | 1 | |||||
| 1 | 1 | |||||
| 1 | 1 | |||||
| 1 | 1 | |||||
| 1 | 1 |
(예시2)
| 1 | 1 | 1 |
에 대해서는 다음 한 가지의 방법 밖에 생각할 수 없다.
| 1 | 1 | 1 |
순서에 대해서[편집]
둘 이상의 다른 숫자가 있는 경우에는 그 순서가 검은 칸의 순서를 나타낸다.
(예시)
| 3 | 1 | |||||
| 1 | 3 |
에 대해서는 정답은 각각 아래와 같다.
| 3 | 1 | |||||
| 1 | 3 |
또한, 가로인 경우만은 나타냈지만 세로일 때도 같다.
(예시)
| 2 |
| 1 |
에 대해서는 세 가지의 방법을 생각할 수 있다.
| 2 | 2 | 2 |
| 1 | 1 | 1 |
기본적인 규칙은 이것뿐이다.
(참조 튜토리얼 : 컨셉티스 아트 로직)
풀 때의 정석[편집]
여기서는 한 열에 10칸이 있는 어느 퍼즐을 푸는 것을 상정하고 있다. 또, 공간 절약을 위해서 가로의 열만을 나타내지만 세로일 때도 같으며 이 곳의 모든 문장을 ‘왼쪽’을 ‘위’로, ‘오른쪽’을 ‘아래’로 바꾸면 세로일 때의 풀이 방법이 된다.
첫 번째 단계[편집]
첫 번째 단계에서는 풀기 시작하는 단계로 아무 단서가 없는 상태이기에 단서가 없이도 풀 수 있는 곳부터 풀어간다. 여기서의 작업을 빼먹으면 도중에 막히기에 확실하게 해야한다.
0과 최고값을 먼저[편집]
먼저 처음에 할 것은 0과 최고값(여기서는 10)부터 처리하는 것이다. 생각할 필요가 없는 0은 모두 빈칸이며 최고값인 경우에는 모두 검은 칸인 것이 확실하기 때문이다.
| 10 |
빈칸인 것이 확정된 칸에는 × 같은 것으로 빈칸이라는 것을 구분시켜둔다. 다만, 너무 크게 표기하면 완성됐을 때의 그림이 보기에 흉해지기에 주의가 필요하다.
| 0 | × | × | × | × | × | × | × | × | × | × |
더해서 최곳값이 되는 것을 풀기[편집]
둘 이상의 숫자가 있는 예시에서 숫자와 숫자 사이에 빈칸이 하나라고 가정하고 계산하면 조금 최곳값과 같은 수가 되는 예시는 하나의 가능성 밖에 없기에 숫자와 숫자 사이에 한 칸만 빈칸을 넣고 나머지는 검은 칸으로 칠한다.
(예시)
| 7 | 2 |
는 7과 2 사이에는 빈칸이 한 칸밖에 없다고 가정하면 7+1+2=10(1은 빈칸 분량, 아래와 같다)이며 최곳값과 같은 값이 되기 때문에 다음의 한가지 방법밖에 없다.
| 7 | 2 | × |
여기서 처리할 수 있는 것은 숫자가 적어질 수록 알아채기 어려워지기에 주의가 필요하다. 예를 들면 아래와 같다.
| 4 | 2 | 2 |
은, 4+1+2+1+2=10이기 때문에,
| 4 | 2 | 2 | × | × |
이다. 더 작은 경우도 있다.
| 1 | 2 | 1 | 1 | 1 |
은, 1+1+2+1+1+1+1+1+1=10이기 때문에,
| 1 | 2 | 1 | 1 | 1 | × | × | × | × |
이다.
좌우에 채울 때에 생기는 공통된 검은 칸을 처리[편집]
예를 들면 다음의 예시를 어떻게 처리할지이다.
| 8 |
이 예시는 다음의 세 가지 방법을 생각할 수 있다.
| 8 | ||||||||||
| 8 | ||||||||||
| 8 |
이 경우에는 더 이상 없는 것인가라고 하면 그렇지도 없다. 잘 보면 어떤 경우나 맨 가운데의 여섯 칸은 반드시 칠해지는 것을 알 수 있다. 따라서, 이 예시는 이처럼 일부가 확정이다.
| 8 |
좀 더 말하면, 맨 왼쪽 칸이 검은 칸이라고 가정하고 가장 오른쪽의 칸이 검은 칸이라고 가정한 경우에 그 두 경우의 공통되는 부분이 검은 칸으로 확정이다.
(예시)
| 6 |
이것을 가장 왼쪽이 검은 칸이라고 가정하면,
| 6 |
반대로 가장 오른쪽이 검은 칸이라고 가정하면,
| 6 |
두 가지 경우를 비교해서 공통으로 검은 칸이 되는 것은,
| 6 |
이 되며, 아래의 예시에서 노란 색으로 표시한 가운데 두 칸이 공통되기에 아래처럼 컴은 칸을 칠한다.
| 6 |
둘 이상의 숫자가 있는 경우에 대해서도 숫자와 숫자 사이에 빈칸을 한 칸이라고 가정하면 같은 작업을 할 수 있다. 단, 왼쪽과 오른쪽부터 칠했을 경우를 비교했을 때에 검은 칸으로 공통되는 부분이 있어도 다른 숫자에서 온 경우에는 공통됐다고 볼 수는 없다(아래의 예시를 참조).
(예시)
| 4 | 2 |
가장 왼쪽이 검은 칸이라고 가정해서,
| 4 | 2 |
가장 오른쪽이 검은 칸이라고 가정해서,
| 4 | 2 |
두 가지의 경우를 비교하면 공통되는 부분이 검은 칸이 되는 것은,
| 4 | 2 |
여기서, 노란 색의 칸은 같은 ‘4’로 칠해져있지만, 초록색 칸은 가장 왼쪽에서 칠했을 경우에는 ‘2’, 가장 오른쪽에서 칠했을 경우에는 ‘4’로 칠해져 있기 때문에 노란 칸만이 확정되는 부분이다. 따라서 다음과 같이 확정이다.
| 4 | 2 |
아래 그림과 같은 경우의 가능성을 고려하면 초록 칸은 확정이 아닌 것을 알 수 있다.
| 4 | 2 |
두 번째 단계[편집]
첫 번째 단계로 확정지을 수 있는 것은 여기까지이다. 후에는 첫 번째 단계에서 확정지은 칸을 단서로 새롭게 확정지을 칸을 늘려가는 작업으로 변한다. 두 번째 단계에서 확정지을 칸도, 새롭게 확정지은 칸을 늘리는 단서가 되기에 다 풀때까지 이 작업을 반복하게 된다. 또한, 이 이후에는 이미 확정지은 검은 칸은 갈색 칸며 이미 확정지은 빈칸은 갈색 칸 안의 ×이며, 새롭게 확정지을 검은 칸과 빈칸은 각각 검은 칸과 검은 ×로 표시하게 된다.
모든 검은 칸, 모든 빈칸이 확정된 예시의 처리[편집]
숫자의 합계와 이미 확정지은 검은 칸의 수가 일치할 경우에 아직 확정 못 지은 칸을 모두 빈칸으로 확정시킨다. 아직 확정 못 지은 칸과 검은 칸으로 확정지은 칸의 합계가 숫자의 합계에 일치한 경우에는 아직 확정 못 지은 칸은 검은 칸으로 확정시킨다.
(예시1)
| 1 |
이 경우, 숫자 ‘1’에 대해서 이미 하나의 검은 칸이 확정되어 있기에 이 이외의 검은 칸은 없다. 따라서,
| 1 | × | × | × | × | × | × | × | × | × |
로 빈칸이 확정된다.
(예시2)
| 1 | 1 | 1 | 1 | × | × | × | × | × | × |
이 경우, 이 예시에는 합계 4칸의 검은 칸이 있는 것이기 때문에 아직 확정 못 지은 칸이 검은 칸이 아니면 검은 칸의 수가 부족해진다. 따라서,
| 1 | 1 | 1 | 1 | × | × | × | × | × | × |
로 검은 칸이 된다.
검은 칸의 이웃 칸 처리[편집]
숫자와 숫자 사이에는 빈칸이 한 칸 이상이 들어가기에 검은 칸이 연속인 것을 알 수 있으면 그 이웃 칸은 빈칸으로 확정한다.
(예시1)
| 1 | 2 | 1 |
이 경우, 이미 칠해진 검은 칸은 ‘2’에서 와서 연속하고 있는 것은 확실하다. 숫자와 숫자 사이에는 반드시 하나 이상의 빈칸이 있기에,
| 1 | 2 | 1 | × | × |
로 빈칸을 확정한다.
(예시2)
| 1 | 2 | 1 |
(예시1)의 경우와 비슷하지만 이번에는 이미 확정지은 칸은 ‘1’에서 온 것인지 ‘2’에서 온 것인지, 이 시점에서는 밝혀지지 않기에 새롭게 확정지을 수 있는 칸은 없다.
가장자리의 처리[편집]
가장 바깥 측이 확정되면 바깥 측의 숫자가 나타내는 검은 칸은 확정이다.
(예시1)
| 3 | 2 |
처럼 가장 왼쪽이 확정짓고 있을 경우에는 자동적으로 ‘3’이 나타내고 있는 것은
| 3 | 2 | × |
로 확정된다. 앞의 항에서 말한 ‘검은 칸의 이웃칸을 처리’에 따라서 왼쪽부터 네 번째에 ×를 붙이는 것도 잊지 않았으면 한다.
(예시2)
| 3 | 2 |
f로, 가장 오른쪽이 확정되었을 경우에는 자동적으로 ‘2’가 나타나고 있는 것은,
| 3 | 2 | × |
로 확정한다. 오른쪽에서 세 번째 ×는 ‘검은 칸의 이웃칸을 처리’에 따른 것이다.
협소한 칸의 처리[편집]
연속되어서 나타나는 숫자보다 협소한 칸의 경우에는 그 부분은 빈칸이라고 확정한다.
(예시1)
| 3 | × |
는, 우측부터 검은 칸을 취하면 두 칸만 나타나기에 우측 끝에는 검은 칸은 넣지 않는다. 따라서
| 3 | × | × | × |
확정한다.
(예시2)
| 3 | × | × |
는, ×와 ×의 사이에는 두 칸만 나타날 수 있기에 거기에는 검은칸은 넣지 않는다. 따라서
| 3 | × | × | × | × |
로 확정한다.
확실히 검은 칸이 닿는 칸, 닿지 않는 칸을 처리[편집]
이미 검은 칸의 확정되어 있으며 숫자와 비교해서 닿지 않는 칸이 있는 경우에는 그 곳은 빈칸으로 확정한다. 또, 몇몇 가장자리에 붙여도 검은 칸이 초과하는 부분에 대해서는 검은 칸으로 확정한다.
(예시1)
| 2 |
이 경우에 가능성은 아래 두 가지밖에 없다.
| 2 | ||||||||||
| 2 |
따라서, 다음처럼 확정한다.
| 2 | × | × | × | × | × | × | × |
(예시2)
| 5 |
이 경우, 우측 끝부터 검은 칸을 했다해도 반드시 오른쪽부터 다섯 번째 칸에 검은 칸이 닿아버린다. 또, 확정되어 있는 칸부터 좌측으로 다섯 칸을 해도 왼쪽부터 세 번째 칸까지 검은 칸은 닿지 않는 것이 명확해진다. 따라서,
| 5 | × | × | × |
로 확정한다.
(예시3)
| 3 | 4 |
이 경우, 우측의 검은 칸부터 좌측에 최대한 네 칸 분량을 늘려줘도 두 개의 검은 칸은 이어지지 않는다. 또, 그 사이에는 규칙에 따라서 최저 하나의 빈칸이 필요하기에 왼쪽부터 네 번째 칸은 4의 칸으로는 채울 수 없다. 그렇게 되면 4의 좌측이 오른쪽으로 벗어나기 때문에(왼쪽부터 다섯 번째 칸), 그 곳부터 오른쪽으로 센 네 번째 칸을 검은 칸으로 확정한다.
| 3 | 4 |
가장자리나 최고값의 갱신에 대한 처리[편집]
바깥 측의 빈칸을 연속해서 확정하면 그 분량만 가장자리가 안 쪽으로 밀리는 것으로 가정할 수 있으며 그에 따라서 그 예시의 최고값이 그것만 적어진다고 가정할 수 있다. 거기서 갱신된 가장자리나 최고값을 사용해서 검은 칸과 빈칸을 확정한다.
(예시1)
| 5 |
이것은, 첫 번째 단계에서는 확정할 수 없었다. 하지만,
| 5 | × |
로 확정한 경우, 오른쪽 끝이 하나 분량의 안쪽으로 어긋난 것을 가정할 수 있으며, 오른쪽에서 두 번째 칸을 새로운 오른쪽 끝으로 생각해서 ‘좌우에 채울 때에 생기는 공통된 검은 칸을 처리’를 진행하면,
| 5 | × |
로 확정할 수 있다.
(예시2)
| 1 | 1 | 1 | 1 |
이것은, 첫 번째 단계에서는 확정할 수 없었다. 하지만,
| 1 | 1 | 1 | 1 | × | × | × |
로 확정하면, 이 열은 최고값이 10에서 7로 내려간 것으로 가정할 수 있다. 그러면, 1+1+1+1+1+1+1=7이 되며, 최고값과 일치하기에,
| 1 | 1 | 1 | 1 | × | × | × | × | × | × |
로 확정한다.
나눠진 칸의 처리[편집]
길고 아무것도 확정되지 않은 칸의 절반쯤을 빈칸으로 확정하면, 그 좌우를 각각 독립해서 처리할 수가 있다.
(예시)
| 3 | 3 |
이것은 첫 번째 단계에서는 확정할 수 없었다. 하지만,
| 3 | 3 | × |
로 확정했을 경우에는 확정된 빈칸의 좌우 어느 한방향으로 모든 검은 칸이 들어가는 것은 있을 수 없기에 좌우 각각 하나씩 들어가게 되며,
| 3 | 3 | × |
로 확정할 수 있다.
세 번째 단계[편집]
문제 중에는 위의 기술을 구사해도 풀 수 없는 경우도 있다.
소거법[편집]
위의 방법만으로 막힌 경우. 주의의 장소를 임시로 모두 칠하는 장소로 가정한다. 게다가 그것을 단서로 문제를 풀어간 경우에 후에 모순점이 생겨버린다면 그곳은 실은 칠해서는 안되는 장소였다는 것을 알게된다.
또한, 모순범이 발생하기까지의 전개가 긴 만큼, 예측하기도 힘들어지며 고전을 강요당할 수 있다. 그러므로, 이 방법은 기술 중에도 고도의 훈련이 요구된다.
게임 “피크로스”, “피크로스 NP”에서는 ‘彫’(“NP”에서는 ‘塗’), ‘×’, ‘消’가 있지만, ‘試し彫り’(“NP”에서는 ‘試し塗り’)마크라는 조작성은 마리오의 슈퍼 피크로스 내에 등장했다.
풀이의 흐름[편집]

|
|
 |
|
 |
|
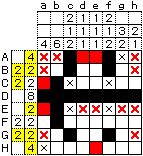 |
|
 |
|
 |
|
 |
|
 |
|
 |
|

|
|
다색화[편집]
기본 규칙으로는 빈칸의 그림만 그릴 수 없기 때문에 둘 이상의 색을 사용할 수 있게 한 규칙도 존재한다.
가장 일반적인 것은 숫자마다 색이 지정되어 있어서 숫자에 지정된 색으로 칠하는 것이다. 이 경우에 같은 열에 숫자가 둘 이상 있어도 다른 색이라면 사이에 공백이 들어가지 않아도 좋다는 규칙이 추가된다(같은 색이라면 기본 규칙처럼 한 칸 이상 비운다).
풀 때에는 아래의 내용에 주의할 필요가 있다.
- 숫자와 숫자 사이에 들어가지 않은 경우가 있기 때문에 확정된 칸이 적어진다.
- 각 색이 어떤 열에서 사용되고 있는지를 확인한다. 이것에 의해서 그 색으로 칠할 수 없는 범위가 나뉘며 그곳에서부터 결정되는 경우가 있다.
문제 만들기[편집]
아직 도트 그림을 그려도 반드시 문제로 성립한다고는 할 수 없다. 답이 하나로 좁히지 않는 경우가 있기 때문이다. 컴퓨터 상에서 문제를 만들 수 있는 소프트웨어 등에서는 문제로 성립하는지 아닌지를 자동적으로 판정해주는 기능이 달려있는 것도 있다.
삼각형 칸[편집]
칠하는 칸을 정사각형을 비스듬히 자른 삼각형으로 한 규칙도 있다. 이러한 것을 다이아몬드 로직 또는 다이아 로직 등으로 불린다[2].
비고[편집]
100×100 칸 등 방대한 칸 수가 되어 오면 칠할 수 있는 칸을 찾는 것이 상당히 힘들어진다.
여기서 첫 번째 단계에서 칠할 수 있는 칸을 계산에 따라서 구할 수 있는 방법이 있다.
- 먼저, 구하고 싶은 행A의 힌트로 나와있는 수를 모두 합한다(이것은 검은 칸의 계산).
- 다음으로 행A의 힌트 개수에 1을 뺀 값을 위에서 계산된 숫자와 합한다(행A가 1, 1 , 3 , 4인 경우에는 3을 더한다. 이것은 빈칸의 합계의 촤저값).
- 마지막으로 칠할 수 있을지를 알고 싶은 수 B(우선은 행A의 높은 수(예시의 경우에는 4)가 좋다)를 모두 합한다.
이 세 개의 단계로 구한 수에서 행A의 칸 수(세로 또는 가로의 칸 수)를 빼서 구한 정수가 첫 번째 단계에서 수 B로 칠할 수 있는 칸 수이다. 0 이하가 됐을 경우에는 행A의 수 B는 첫 번째 단계에서는 칠할 수 없다. 칠하는 위치는 첫 번째 단계의 풀이 방법을 참조.
덧붙여서 열의 경우에는 행A가 15칸일 시에는 4의 부분에 한 칸을 칠할 수 있으며, 14칸이였던 경우에는 3의 한 칸과 4의 두 칸의 합계 세 칸을 칠할 수 있다.
예시[편집]
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
각주[편집]
- ↑ Dalgety, James, History of Grid Puzzles http://puzzlemuseum.com/griddler/gridhist.htm Retrieved 2013-12-18
- ↑ 예를 들면 일본 문예사의 “일러스트 로직”에서는 ‘다이아 로직’의 이름으로 빈번히 출제되고 있다.
