아녜시의 마녀
기하학에서 아녜시의 마녀(Agnesi-魔女, 영어: witch of Agnesi)는 대수 곡선의 하나이다. 마리아 아녜시의 이름을 땄다.
정의[편집]
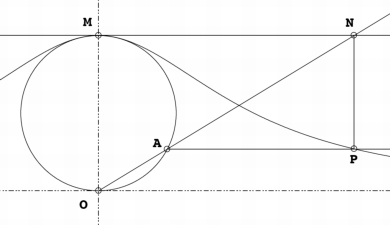
좌표평면에서 중심이 (0, a)이고 반지름이 a인 원을 생각하자. 점 (0, 0)을 지나는 직선은 이 원과 점 A에서 만나며, 직선 y=2a 위의 점 N에서 이 직선과 만난다. A를 지나는 수평선과 N을 지나는 수직선을 그리면 교점 P를 구할 수 있다. 아녜시의 마녀는 점 P의 자취이다.
직선 OA와 y축 사이의 각 θ를 이용하여 아녜시의 마녀의 방정식을 나타낼 수 있다. P의 좌표를 (x, y)라고 하자. 그러면∠OAM=90˚이고, OM는 원의 지름이다. 직각삼각형 OAM의 성질에 의하여
를 얻는다. 점 A, N을 각각 x축에 사영(projection)한 점을 R, S라고 하자. 그러면 ONS는 직각삼각형이므로 OS = x = NS tanθ = 2a tanθ가 성립하고, OAR이 직각삼각형이므로 를 얻는다. 따라서 아녜시의 마녀의 방정식은
가 된다.
여기서 x와 y의 관계식을 찾으려면 위 식의 θ를 소거해야 한다. 등식 를 이용하면 다음을 얻는다.
이 식으로부터 여러 가지 성질을 이끌어낼 수 있다. 먼저 x → ±∞일 때 y → 0이므로, 이 곡선은 x축을 점근선으로 가진다. 둘째, 이 곡선과 점근선 사이의 넓이는 이다. 즉 원의 넓이의 4배이다. 또한, 이 곡선은 θ=±π/6에서 2개의 변곡점을 가짐을 알 수 있다.
역사[편집]
아녜시의 마녀는 아녜시가 처음 발견한 것은 아니다. 이 곡선은 이미 피에르 드 페르마와 루이지 귀도 그란디(이탈리아어: Luigi Guido Grandi, 1671–1742)에 의하여 연구된 바 있었다. 그란디는 이를 ‘곡선’을 뜻하는 단어 이탈리아어: versiera 베르시에라[*]라고 불렀고, 아녜시도 저서 이탈리아어: Instituzioni analitiche ad uso della gioventù italiana에서 마찬가지로 이탈리아어: versiera라고 불렀다.
존 콜슨(영어: John Colson)이 아녜시의 책을 영어로 번역할 때 이탈리아어: versiera 베르시에라[*]를 이탈리아어: aversiera(적(敵), 악마 또는 마녀 [신의 적])로 혼동하여 ‘마녀’로 오역하였다. 그 뒤 이 곡선은 ‘아녜시의 마녀’로 불리게 되었다.
기타[편집]
아녜시 탄생 296주년 기념으로 구글 doodle에 올라갔다
외부 링크[편집]
- Weisstein, Eric Wolfgang. “Witch of Agnesi”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- O'Connor, John J.; Edmund F Robertson. “Witch of Agnesi” (영어).






