서포트 벡터 머신
| 기계 학습과 데이터 마이닝 |
|---|
 |

서포트 벡터 머신(support vector machine, SVM[1][2])은 기계 학습의 분야 중 하나로 패턴 인식, 자료 분석을 위한 지도 학습 모델이며, 주로 분류와 회귀 분석을 위해 사용한다. 두 카테고리 중 어느 하나에 속한 데이터의 집합이 주어졌을 때, SVM 알고리즘은 주어진 데이터 집합을 바탕으로 하여 새로운 데이터가 어느 카테고리에 속할지 판단하는 비확률적 이진 선형 분류 모델을 만든다. 만들어진 분류 모델은 데이터가 사상된 공간에서 경계로 표현되는데 SVM 알고리즘은 그 중 가장 큰 폭을 가진 경계를 찾는 알고리즘이다. SVM은 선형 분류와 더불어 비선형 분류에서도 사용될 수 있다. 비선형 분류를 하기 위해서 주어진 데이터를 고차원 특징 공간으로 사상하는 작업이 필요한데, 이를 효율적으로 하기 위해 커널 트릭을 사용하기도 한다.
목표 및 아이디어[편집]
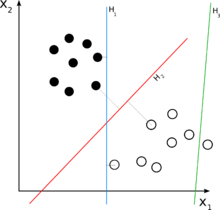
데이터를 분류하는 것은 기계학습에 있어서 일반적인 작업이다. 주어진 데이터 점들이 두 개의 클래스 안에 각각 속해 있다고 가정했을 때, 새로운 데이터 점이 두 클래스 중 어느 곳에 속하는지 결정하는 것이 목표이다. 서포트 벡터 머신에서, 데이터 점이 -차원의 벡터 (개의 숫자 리스트)로 주어졌을 때, 이러한 데이터 점을 -차원의 초평면으로 분류할 수 있는지를 확인하고 싶은 것이다. 이러한 작업을 선형 분류라고 말한다. 데이터를 분류하는 초평면은 여러 경우가 나올 수 있다. 초평면을 선택하는 타당한 방법 중 하나는 두 클래스 사이에서 가장 큰 분류 또는 마진(margin)을 가지는 초평면을 선택하는 것이다. 그래서 우리는 초평면에서 가장 가까운 각 클래스의 데이터 점들 간의 거리를 최대로 하는 초평면을 선택한다. 만약 그런 초평면이 존재할 경우, 그 초평면을 최대-마진 초평면(영어: maximum-margin hyperplane) 이라 하고 선형 분류기를 최대-마진 분류기(영어: maximum margin classifier)라고 한다.
선형 SVM[편집]
주어진 학습용 데이터 집합 D(N 개의 점으로 이루어진 집합)를 다음과 같이 정의해보자.
각 는 p차원의 실수 벡터이고 , 는 가 어떤 클래스에 속해있는지를 나타내는 값으로 1 혹은 -1의 값을 가진다.
위의 학습용 데이터 집합이 값에 따라 선형적으로 분리될 수 있을 때, 데이터 집합을 분리하는 것을 초평면이라 하며 다음의 조건을 만족하는 점 X의 집합으로 나타낼 수 있다.
은 내적 연산자이고, 은 초평면의 법선 벡터(normal vector)이다.
주어진 초평면의 서포트 벡터(+, -)는 다음과 같이 정의된다.
- + : 의 데이터중에서 초평면과 가장 가까운 데이터
- - : 의 데이터중에서 초평면과 가장 가까운 데이터
주어진 초평면과 같은 법선벡터를 가지면서 +를 지나는 초평면은
으로 나타낼 수 있고 비슷한 방식으로 -를 지나는 초평면은
이와 같이 나타낸다.
초평면의 마진은 각 서포트 벡터를 지나는 초평면 사이의 거리를 의미한다. 기하학적으로 두 초평면 사이의 거리 즉, 마진을 구하면 라는 것을 알 수 있으며 서포트벡터머신은 마진을 최대로 만드는 알고리즘이다.
서포트벡터를 지나는 초평면 사이엔 데이터 포인트가 존재하지 않아야 하므로 다음과 같은 식이 성립한다.
- 인 에 대해서
- 인 에 대해서
위 두 식은 아래와 같은 식으로 나타낼 수 있다.
초평면의 조건을 따르며 마진의 최댓값을 구하고자 하는 서포트 벡터 머신 문제는 다음과 같은 최적화 문제로 표현할 수 있다.
- 단,
원 형식[편집]
위에서 설명한 최적화 문제는 의 노름인 이 제곱근을 포함하고 있기 때문에 풀기 어렵다. 위의 최적화 문제에서 를 로 치환하여도 최적화 문제를 만족시키는 해 , 는 변하지 않는다. 또한 로 치환을 하게 되면 위의 문제는 2차 계획법(영어: quadratic programming 쿼드라틱 프로그래밍[*]) 최적화 문제가 된다. 치환된 최적화 문제는 아래와 같이 나타낼 수 있다.
- 단,
라그랑주 승수법을 이용하면 위의 문제를 다음과 같은 안장점(영어: saddle point)을 찾는 문제로 나타낼 수 있다.
안장점을 찾는 과정에서 으로 분류될 수 있는 모든 점들은 그에 대응하는 가 0으로 지정되기 때문에 영향을 미치지 않는다. 이제 이 문제는 정규 2차 계획법 기법으로 해결할 수 있다. 정적 Karush-Kuhn-Tucker 조건에 따르면, 문제의 해는 훈련 벡터(영어: training vector)의 선형 조합으로 표현될 수 있다.
적은 수의 만이 0보다 큰 값을 가지고, 그에 대응하는 들은 를 만족하는 정확한 서포트 벡터이다. 이 식을 통해 다음과 같이 오프셋 (컴퓨터 과학) 에 대한 정의를 유도할 수 있다.
는 와 에 의존하므로 각각의 데이터 포인트마다 값이 다르다. 표본 분포의 평균은 모평균(population mean)에 대해 불편 추정량이므로 다음과 같이 모든 서포트 벡터 에 대해서 평균을 취하는 것이 좋다.
쌍대 형식[편집]
분류 규칙을 비제약 쌍대 형식으로 나타내면, 최대 마진 초평면과 분류 작업이 오직 마진 위에 놓여있는 서포트 벡터들로부터만 영향을 받는다는 것을 알 수 있다. 에서 로 치환하면 SVM의 쌍대 형식이 다음과 같은 최적화 문제로 바뀐다.
- 를 최대화 하라.
- 단,
여기서 는 를 최소화하는 과정에서 생기는 제약이다.
커널은 로 정의된다.
는 항에 의해서 계산될 수 있다:
편향된 초평면과 비편향된 초평면[편집]
필요에 의해서 초평면이 좌표계의 원점을 지나야하는 경우가 존재한다. 이때 원점을 지나는 초평면을 비편향된 초평면이라 말하며, 그렇지 않은 초평면은 편향된 초평면이라 말한다. 원 형식에선 의 조건을 줌으로써 비편향된 초평면을 구할 수 있고, 이에 대응되는 쌍대 형식은 위에서 제시된 쌍대 형식에서 의 조건을 풀어줌으로써 구할 수 있다.
소프트 마진[편집]
1995년에 Corinna Cortes와 Vladimir N. Vapnik은 잘못 분류된 자료들을 허용하는 변형된 최대 마진 분류기 아이디어를 제안했다.[1] 만약 “네” 또는 “아니오”라는 결과를 내야하는 자료들을 분할하는 초평면이 존재하지 않는다고 하자. 그러면 소프트 마진 방법은 여전히 가장 가까이 위치해 있는 제대로 분리되는 자료들의 거리를 최대화하면서, 주어진 자료들을 가능한 한 제대로 분리하는 초평면을 찾을 것이다. 이 방법은 음수가 아닌 느슨한 변수(영어: slack variable) 를 이용하는데, 이 변수는 자료 가 잘못 분류된 정도를 나타낸다.
그러면 목적함수는 0이 아닌 에 대해 페널티를 부과하는 함수에 의해서 증가된다. 그에 따른 최적화는 마진을 크게 하는 것과 에러에 대한 페널티를 작게 하는 것의 균형을 맞추는 것이 된다. 만약 페널티를 부과하는 함수가 선형이라면, 최적화 문제는 다음과 같이 된다.
- 단,
다변수 적응 회귀 스플라인(영어: Multivariate Adaptive Regression Splines, MARS)에서와 같이 경첩 함수(영어: hinge function) 표기법을 이용하면, 이 최적화 문제는 다음과 같이 쓰일 수 있다.
- 일 때,
(2)에서의 제약조건은 목적함수에서 를 최소화하는 것과 함께 라그랑주 승수법을 이용하여 위에서와 마찬가지로 해결될 수 있다. 그러면 다음의 문제를 해결해야 한다.
- 단,

듀얼 형식[편집]
- 를 최대화하라.
- 단,
선형 페널티 함수의 핵심 장점은 상수 C가 오직 라그랑주 승수법의 추가적인 제약조건에 등장함으로써, 듀얼 문제에서는 느슨한 변수가 사라진다는 점이다. 위의 공식화와 이것의 실제상황에서 미치는 큰 영향에 대해서 Cortes와 Vapnik은 2008년에 ACM Paris Kanellakis Award를 수상하였다.[3] 비선형 페널티 함수들도 특히 분류기에서 이상치(영어: outliers)의 효과를 줄이는데 사용되고 있다. 그러나 이를 사용하는데 주의를 기울이지 않는다면 문제는 볼록하지 않게(영어: non-convex) 되고, 그러면 이는 전역해(영어: global solution)를 찾는데 상당히 어려운 문제가 된다.
비선형 분류[편집]
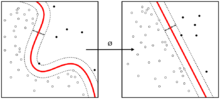
최적의 초평면을 구하는 알고리즘의 시초는 1963년도 vapnik이 제안한 선형 분류였다. 하지만 1992년에 Bernhard E. Boser, Isabelle M. Guyon and Vladimir N. Vapnik 이 최대 마진 초평면 문제에 커널 트릭을 적용해서 비선형 분류를 제안하였다.[4][5] 비선형 분류 알고리즘은 기존의 선형 분류 알고리즘과 형태상으로 비슷하지만 내적 연산이 비선형 커널 함수로 대체된다. 이를 통해 변환된 특징 공간 (feature space)의 최대 마진 초평면 문제 해결을 할 수 있었다. 여기서 말하는 변환은 비선형 변환이거나 차원을 높이는 변환이 될 수 있다. 즉, 분류기는 고차원 특징 공간에서 선형 초평면이지만 기존 차원 공간 상에선 비선형 초평면이 된다. 만약 가우시안 방사 기저함수 (Gaussian radial basis function)를 커널 함수를 적용한다면 특징 공간은 무한 차원의 힐버트 공간(Hilbert space)이 된다.
최대 마진 분류는 많은 연구를 통해 조정되어왔다. 또한 고차원 공간을 이용한 분류는 기존 공간에서의 잘못된 분류 결과를 내지는 않을 것이라고 생각되어왔다. 하지만 고차원 공간에서의 분류는 기존 공간에서의 분류 일반화의 오차를 상승시킨다는 것이 증명되었고 그 상승 폭에 대한 임계 값이 있다는 것 역시 알려져 있다.[6]
다음과 같은 일반적인 커널들이 있다.
- 동차다항식(영어: Homogeneous polynomial):
- 다항식 커널(영어: Polynomial kernel)(Inhomogeneous):
- 가우시안 방사 기저 함수(영어: Gaussian radial basis function): . 때때로 으로도 나타낸다.
- 쌍곡탄젠트(영어: Hyperbolic tangent): ,
커널은 변환 와 다음과 같이 연관되어 있다. .
w의 값 또한 변환된 공간에 다음과 같이 존재한다. .
분류를 위해서 w와 내적을 구할 때는 다음과 같은 커널 트릭을 이용해 계산할 수 있다. .
하지만, 일반적인 경우에 를 만족하는 w'는 존재하지 않는다.
적용[편집]
SVM은 다음과 같은 현실 세계의 문제들을 해결하는데 사용된다:
- SVM은 텍스트와 하이퍼텍스트를 분류하는데 있어서, 학습 데이터를 상당히 줄일 수 있게 해준다.
- 이미지를 분류하는 작업에서 SVM을 사용할 수 있다. SVM이 기존의 쿼리 개량 구조보다 상당히 높은 검색 정확도를 보인 것에 대한 실험 결과가 있다.
- SVM은 분류된 화합물에서 단백질을 90%까지 구분하는 의학 분야에 유용하게 사용된다.
- SVM을 통해서 손글씨의 특징을 인지할 수 있다.
서포트 벡터 머신 라이브러리[편집]
여러 프로그래밍 언어에 지원되는 서포트 벡터 머신 라이브러리 목록
C/C++[편집]
- C로 구현된 서포트 벡터 머신 코드이다. 무료로 다운받아서 사용할 수 있으며, Windows, Mac OS X, Linux, Cygwin, 그리고 Solaris에서 사용 가능하다.
- C로 구현된 서포트 벡터 머신 코드이다. SVM light를 최적화하는데 기반을 두고있다. 무료로 다운받아서 사용할 수 있으며, Windows와 Linux에서 사용 가능하다.
- LIBSVM.[7] ( http://www.csie.ntu.edu.tw/~cjlin/libsvm/ )
- 파이썬에서의 LIBSVM과 같다.
- C++로 구현된 코드로, 이진 분류를 위한 큰 규모의 서포트 벡터 머신을 위해 설계된 코드이다. 무료로 다운받아서 사용할 수 있으며, Linux에서 사용 가능하다.
Python[편집]
- scikit-learn ( https://web.archive.org/web/20150418093915/http://scikit-learn.org/stable/index.html )
- 파이썬에서 머신 러닝 기법들을 사용하는데 도움을 주는 라이브러리이다. scikit-learn은 NumPy, SciPy, 그리고 matplotlib 라이브러리들을 기반으로 구현되었고 오픈 소스이며 상업적으로도 이용 가능하다. Windows, Mac OS X, 그리고 Linux에서 사용 가능하다.
- 파이썬에서 머신 러닝 기법들을 사용하는데 도움을 주는 라이브러리이다. 하지만 PyML은 scikit-learn이 전반적인 머신 러닝 기법들을 제공해주는데 비해, PyML은 서포트 벡터 머신 기능에 초점을 맞추고 있다. 무료로 다운받아서 사용할 수 있으며, Linux와 Mac OS X에서 사용 가능하다.
- LIBSVM ( http://www.csie.ntu.edu.tw/~cjlin/libsvm/ )
- 서포트 벡터 머신만을 위한 라이브러리로 파이썬 뿐만 아니라 C/C++, Java, Matlab, R, Perl 등의 다양한 언어를 지원한다. 무료로 다운받아서 사용할 수 있으며, Windows, Mac OS X, 그리고 Linux에서 사용 가능하다.
Java[편집]
- LIBSVM ( http://www.csie.ntu.edu.tw/~cjlin/libsvm/ )
- 파이썬에서의 LIBSVM과 같다.
MATLAB[편집]
- LIBSVM ( http://www.csie.ntu.edu.tw/~cjlin/libsvm/ )
- 파이썬에서의 LIBSVM과 같다.
- Matlab SVM Toolbox ( https://web.archive.org/web/20150421234040/http://www.isis.ecs.soton.ac.uk/resources/svminfo/ )
- 매트랩으로 구현한 서포트 벡터 머신이다. 서포트 벡터 머신을 이용한 분류와 회귀 기능을 제공하고 그래픽 사용자 인터페이스도 제공한다. 무료로 다운받아서 사용할 수 있다.
- 매트랩에서 머신 러닝 기법을 사용하는데 도움을 주는 패키지이다. 무료로 다운받아서 사용할 수 있다.
- LS-SVMlab ( https://web.archive.org/web/20150513103825/http://www.esat.kuleuven.be/sista/lssvmlab/ )
- 기존의 표준적인 서포트 벡터 머신을 재공식화한 최소제곱법 서포트 벡터 머신을 구현한 매트랩 라이브러리이다. 무료로 다운받아서 사용할 수 있으며, Windows와 Linux에서 사용 가능하다..
- 매트랩으로 구현되었고, 다양한 버전의 서포트 벡터 머신을 지원한다. 무료로 다운받아서 사용할 수 있으며, 매트랩 파일 형식으로 제공된다.
R[편집]
- e1071( https://web.archive.org/web/20180714040902/http://cran.r-project.org/web/packages/e1071/e1071.pdf )
- 파이썬에서의 LIBSVM과 같다.
참조[편집]
- ↑ 가 나 Cortes, C.; Vapnik, V. (1995). “Support-vector networks”. 《Machine Learning》 20 (3): 273. doi:10.1007/BF00994018.
- ↑ *Vapnik, V. (2000). 〈Section 5.6. Support Vector Machines〉. 《The nature of statistical learning theory》. New York: Springer-Verlag New York. ISBN 978-1-4419-3160-3.
- ↑ ACM Website, Press release of March 17th 2009. http://www.acm.org/press-room/news-releases/awards-08-groupa Archived 2010년 12월 30일 - 웨이백 머신
- ↑ Aizerman, Mark A.; Braverman, Emmanuel M.; and Rozonoer, Lev I. (1964). “Theoretical foundations of the potential function method in pattern recognition learning”. 《Automation and Remote Control》 25: 821–837.
- ↑ Boser, B. E.; Guyon, I. M.; Vapnik, V. N. (1992). 〈A training algorithm for optimal margin classifiers〉. 《Proceedings of the fifth annual workshop on Computational learning theory - COLT '92》. 144쪽. doi:10.1145/130385.130401. ISBN 089791497X.
- ↑ Jin, Chi; Wang, Liwei (2012). 《Dimensionality dependent PAC-Bayes margin bound》. Advances in Neural Information Processing Systems.
- ↑ Chang, Chih-Chung (2011). “LIBSVM: A library for support vector machines”. 《Machine Learning》 2 (3). doi:10.1145/1961189.1961199.

























![{\displaystyle \arg \min _{\mathbf {w} ,b}\max _{{\boldsymbol {\alpha }}\geq 0}\left\{{\frac {1}{2}}\|\mathbf {w} \|^{2}-\sum _{i=1}^{n}{\alpha _{i}[y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1]}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad97bd476df655aa873c8a10dac38f7c2c202c6d)





















![{\displaystyle [1-y_{i}(w\cdot x_{i}+b)]_{+}=[\xi _{i}]_{+}=\xi _{i},\quad \lambda =1/2C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/614a657b891b9752dd884edacfb4b11e0f63ebab)
![{\displaystyle \sum _{i}[1-y_{i}(w\cdot x_{i}+b)]_{+}+\lambda \|w\|^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/423fcb51ba33b7864bb9086e00d051878d1c85b4)
![{\displaystyle \arg \min _{\mathbf {w} ,\mathbf {\xi } ,b}\max _{{\boldsymbol {\alpha }},{\boldsymbol {\beta }}}\left\{{\frac {1}{2}}\|\mathbf {w} \|^{2}+C\sum _{i=1}^{n}\xi _{i}-\sum _{i=1}^{n}{\alpha _{i}[y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1+\xi _{i}]}-\sum _{i=1}^{n}\beta _{i}\xi _{i}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/278ced35799276e0c48492e70826e5facc49e778)


















