라이먼 계열
물리와 화학에서 라이먼 계열(Lyman series)은 전자가 n≥2(n은 주 양자수)에서 n=1로 전이하면서 나타나는 수소 스펙트럼 계열의 자외선 방출 스펙트럼이다. 전이의 이름은 그리스 문자 순서대로 붙었다. (n=2에서 n=1로 갈 때 Lyman-alpha로 불린다. 3에서 1로 갈때 Lyman-beta, 4에서 1로 갈때 Lyman-gamma,등.) 계열의 이름은 발견자의 이름 시어도어 라이먼에서 따온 것이다.
역사[편집]
라이먼 계열의 스펙트럼에서 첫 번째 선은 하버드 물리학자 시어도어 라이먼(Theodore Lyman)이 1906년에 발견하였다. 그는 전자가 들뜬 수소 가스 전자의 자외선 스펙트럼을 연구하였다. 스펙트럼선의 그밖의 것들은(모두 자외선 영역) 1906년부터 1914년 사이에 라이먼이 발견하였다.
수소에 의한 방출 스펙트럼은 연속적이지 않다. 수소 방출선의 첫 계열의 예가 여기에 있다.
역사적으로, 수소 스펙트럼의 성격을 설명하는 것은 물리학에서 중요한 문제였다. 1885년에 가시광선 영역의 수소 스펙트럼에 해당하는 경험적 수식인 발머 식을 발견하기 전까지 수소선들의 파장은 누구도 예견하지 못했다. 5년에 걸쳐 요하네스 뤼드베리가 이 문제를 풀어 경험적 수식을 설명할 수 있었다. 1888년에 처음으로 발표하고 1890년에 최종적으로 발표하였다.
뤼드베리는 발머 계열 방출선과 잘 어울리는 수식을 찾았으며 아직 발견되지 않은 계열의 방출선도 예언했다. 뤼드베리 공식의 특정한 자연수를 바꿈으로 나타나는 다른 형태들에서 다른 방출선들이 도출되었다.
라이먼 계열[편집]
아래 형태의 뤼드베리 공식은 라이먼 계열을 만들어낸다.
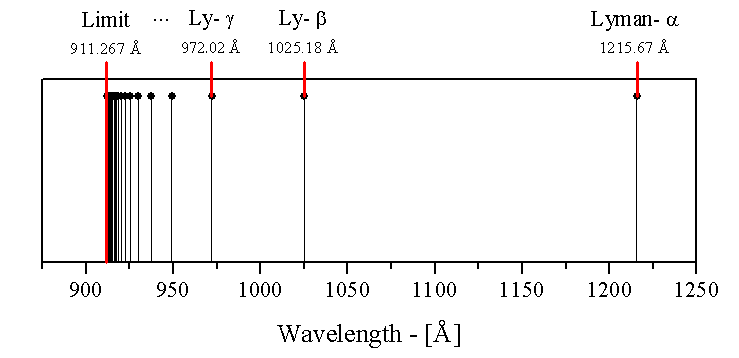
n은 2와 같거나 큰 자연수이다.(i.e. n=2,3,4,....) 그러므로 이미지의 선들은 n=2에 해당하는 파장은 오른쪽에 나타나고, n=∞ 는 왼쪽에 나타난다. ( 그곳에는 무한히 많은 스펙트럼 선이 있다. 그러나 그것들이 매우 밀도가 높으면 n=로 접근한다. 그러므로 처음 선의 몇몇과 마지막 하나에 나타난다.) Lyman series안의 파장에서 모든 자외선:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
| Wavelength (nm) | 121.6 | 102.5 | 97.2 | 94.9 | 93.7 | 93.0 | 92.6 | 92.3 | 92.1 | 91.9 | 91.15 |
연구와 파생[편집]
1913년 닐스 보어는 보어 모형 이론을 만들었다. 수소 스펙트럼선이 뤼드베리의 수식에 맞아떨어지는 이유를 설명하였다. 보어에 따르면 수소 원자와 결합한 전자의 에너지는 반드시 양자화된 레벨로 나타나며 아래의 공식으로 나타낼 수 있다.
보어의 세 번째 가정에 따르면 초기 에너지 레벨(Ei)에서 마지막 에너지 레벨(Ef)로 떨어지는 전자는 언제나 다음 파장의 방출선을 가진다.
에너지 단위를 전자볼트로, 파장을 옹스트롬으로 해서 더 편하게 나타낼 수 있다.
에너지를 위의 수소 원자 에너지 표현으로 대신하고, 초기 상태의 에너지 레벨은 n, 마지막 상태의 에너지는 m으로 나타내면 다음과 같다.
는 뤼드베리의 긴 수식에서 뤼드베리 상수와 같다.
보어, 뤼드베리, 라이먼의 결과들을 연결하려면, m을 1로 두면 된다.
그 결과 라이먼 계열 뤼드베리 공식이 도출되었다. 그러므로 흡수선의 각각의 파장은 전자의 어떤 에너지 레벨(1보다 크다)에서 처음 에너지 레벨로 떨어지는 것을 따른다.




![{\displaystyle E_{n}=-{{me^{4}} \over {2\left(4\pi \varepsilon _{0}\hbar \right)^{2}}}{1 \over n^{2}}=-{13.6 \over n^{2}}[{\mbox{eV}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8b141e2b5d88cb0dbbcc3c3ec06c6d7afc790bb)




