힐베르트 호텔

힐베르트 호텔

힐베르트 호텔 역설은 수학에서 무수히 많은 방이 있는 호텔에 손님이 가득 차 있을 때는 몇 명의 손님이 더 오더라도 손님들의 방을 재배열하여 새로운 손님이 투숙할 공간을 마련할 수 있다는 내용의 사고실험이다.

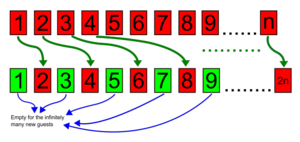
무수히 많은 방이 있는 호텔에는 각 방마다 번호 1, 2, 3, ... 이 붙어있다. 이 호텔에 손님이 가득 찼던 어느날 한 명의 손님이 찾아왔다. 손님이 가득 차서 새로온 손님이 투숙하는 것이 불가능해 보이지만, 관리인은 1번방의 손님은 2번방으로, 2번방의 손님은 3번방으로... 기존의 손님들의 방을 재배열하여 1번방이 비게 한 후에 새로 온 손님이 1번방에 투숙하는 것이 가능하도록 하였다. 이 호텔에 손님이 가득 찼던 또 다른 어느날 이번엔 무수히 많은 손님이 찾아왔다. 손님이 가득 차서 새로운 손님이 투숙하는 것이 불가능해 보이지만, 관리인은 1번방의 손님은 2번방으로, 2번방의 손님은 4번방으로.... 일반적으로 각각의 방에 있던 손님을 그 방번호의 두 배의 방번호를 가진 방으로 배정하여 무수히 많은 빈 방을 새로 마련하였다.

이번에는 무수히 많은 팀이 투숙을 하기 위해 찾아왔는데, 각 팀은 무수히 많은 멤버를 데리고 있다. 그렇지만, 이번 경우에도 관리인은 교묘하게 손님들을 배열하여 투숙하게 하였다. 먼저 이미 방을 차지하고 있는 손님들은 원래 방 번호의 두 배의 방번호를 가진 방으로 배정하였다. 그리고 새로 온 각 팀에 번호를 부여하고, 팀 내 멤버에도 별도의 번호를 부여한 후 팀 번호 번째 홀수 소수의 멤버 번호 제곱 방 번호를 가진 방으로 배정하였다. 예컨데, 두 번째 팀의 네 번째 멤버는 두 번째 홀수 소수인 5의 네제곱, 즉, 625번방에 배정하였다.