중점연결정리
보이기
기하학에서 중점연결정리(中點連結定理)는 삼각형 또는 사다리꼴에 관한 정리이다.
삼각형의 중점연결정리
[편집]삼각형의 두 변의 중점을 연결한 선분은 나머지 변과 평행하고, 그 길이는 나머지 변의 길이의 이다.

증명
[편집]ABC와 ADE에서
- ∠A는 공통
∴ABC ADE (SAS 닮음)
∴∠ADE=∠ABC
즉, DE//BC
또, 이므로
역
[편집]- 삼각형의 한 변의 중점을 지나서 다른 한 변에 평행한 직선은 나머지 한 변의 중점을 지난다.
사다리꼴에서의 중점연결정리
[편집]일 때
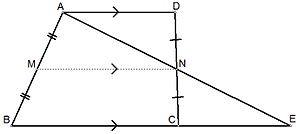
증명
[편집]AN과 BC의 연장선의 교점을 E라 할 때
ADN와 ECN에서
- DN=NC (가정)
- ∠AND=∠ENC (맞꼭지각)
- ∠ADN=∠ECN (엇각)
∴ADN ≡ECN (ASA 합동)
∴ AN=NE, AD=CE
그러므로 ABE에서 중점연결정리에 의하여
같이 보기
[편집]| 이 글은 기하학에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. |










