유의 확률
이 문서의 내용은 출처가 분명하지 않습니다. (2010년 9월) |
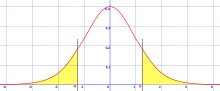

통계적 가설 검정에서 유의 확률(有意 確率, 영어: significance probability, asymptotic significance) 또는 p-값(영어: p-value, probability value)은 귀무가설이 맞다고 가정할 때 얻은 결과보다 극단적인 결과가 실제로 관측될 확률이다. 실험의 유의확률은 실험의 표본 공간에서 정의되는 확률변수로서, 0~1 사이의 값을 가진다.
p-값(p-value)은 귀무 가설(null hypothesis)이 맞다는 전제 하에, 표본에서 실제로 관측된 통계치와 '같거나 더 극단적인' 통계치가 관측될 확률이다. 여기서 말하는 확률은 '빈도주의' (frequentist) 확률이다.
p-값(p-value)는 관찰된 데이터가 귀무가설과 양립하는 정도를 0에서 1 사이의 수치로 표현한 것이다. p-value가 작을수록 그 정도가 약하다고 보며, 특정 값 (대개 0.05나 0.01 등) 보다 작을 경우 귀무가설을 기각하는 것이 관례이나 여기에는 여러 가지 문제들이 있다.[1] 이러한 문제들로부터 일단의 과학자들은 유의확률(P값)을 0.05의 관례에서 0.005로 높일것을 권고하는 개선안의 실시를 촉구한 바 있다.[2] 이러한 재정의에 따른 교정의 효과는 기존의 0.05~0.005의 P값을 '제안적 증거'(suggestive evidence)로 표현하고 0.005 이하의 P값에서 '유의미'(significant)하다는 표현을 사용할 것으로 권고하고 있다. 한편 과학계는 기존 논문의 유의미성을 제고하기 위한 또다른 방안으로 가설의 재실현성을 언급한 바 있다.
정의[편집]
주어진 표본의 유의 확률은 귀무가설을 가정하였을 때 표본 이상으로 극단적인 결과를 얻을 확률이다. 여기서 "더 극단적"이라는 것은 정의에 따라 다르다. 예를 들어, 정규분포의 경우, 귀무가설을 가정한 실수 확률변수 와 표본 에 대하여 왼쪽 꼬리 유의 확률(영어: left-tail p-value)
및 오른쪽 꼬리 유의 확률(영어: right-tail p-value)
및 양쪽 꼬리 유의 확률(영어: double-tail p-value)
를 정의할 수 있다.
만약 확률 변수가 단순한 실수가 아니라면, 더 복잡한 "극단성"을 정의하여야 한다. 예를 들어, 표본이 노름공간에 있는 경우, 노름함수 를 사용하여 표본 의 유의 확률을
로 정의할 수 있다.
같이 보기[편집]
각주[편집]
- ↑ Ronald L. Wasserstein & Nicole A. Lazar (2016). “The ASA's Statement on p-Values: Context, Process, and Purpose”. 《The American Statistician》. 2020년 6월 18일에 원본 문서에서 보존된 문서. 2018년 4월 22일에 확인함.
- ↑ (Nature Human Behavior- Redefine Statistical Significance ,Daniel J. Benjamin,James O. Berger,70 etc, DOI 10.31234/osf.io/mky9j ,Abstract-"We propose to change the default P-value threshold for statistical significance for claims of new discoveries from 0.05 to 0.005.")https://psyarxiv.com/mky9j/
외부 링크[편집]
- Weisstein, Eric Wolfgang. “P-value”. 《Wolfram MathWorld》 (영어). Wolfram Research.
| 이 글은 수학에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. |








