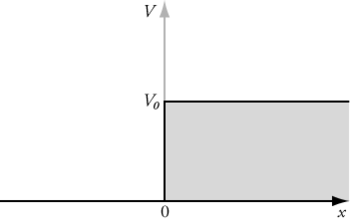
퍼텐셜 계단 (step potential)은 양자역학 과 산란이론 에서 쓰이는 모델 시스템이다. 단 모양의 퍼텐셜 에서의 입자에 대한 시간에 무관한 슈뢰딩거 방정식 을 푸는 것으로 구성되어 있고, 보통 이 모델의 퍼텐셜은 헤비사이드 계단함수 로 나타낸다.
1차원 퍼텐셜 단 [ 편집 ] 퍼텐셜 [ 편집 ] 퍼텐셜 단 1차원 퍼텐셜 단의 퍼텐셜은 다음과 같이 헤비사이드 계단함수 로 주어진다.
V
(
x
)
=
V
0
θ
(
x
)
{\displaystyle V(x)=V_{0}\theta (x)\;}
여기서
θ
(
x
)
=
{
0
x
<
0
1
x
>
0
{\displaystyle \theta (x)=\left\{{\begin{matrix}0&x<0\\1&x>0\end{matrix}}\right.}
일반해 [ 편집 ] 경계조건을 무시하고 시간에 무관한 슈뢰딩거 방정식을 풀면 아래와 같은 파동함수를 얻는다.
ψ
(
x
)
=
{
A
e
i
k
x
+
B
e
−
i
k
x
x
<
0
C
e
i
k
′
x
+
D
e
−
i
k
′
x
x
>
0
{\displaystyle \psi (x)=\left\{{\begin{matrix}Ae^{ikx}+Be^{-ikx}&x<0\\Ce^{ik'x}+De^{-ik'x}&x>0\end{matrix}}\right.}
여기서,
k
2
=
2
m
E
ℏ
2
{\displaystyle k^{2}={2mE \over \hbar ^{2}}\;}
k
′
2
=
2
m
(
E
−
V
0
)
ℏ
2
{\displaystyle k'^{2}={2m(E-V_{0}) \over \hbar ^{2}}\;}
이다.
경계조건 [ 편집 ] 시간에 무관한 슈뢰딩거 방정식에 의하면 각 점에서 파동함수와 파동함수의 1차미분이 연속이여야 한다. 즉, 여기서는 파동함수에 대해
ψ
(
0
−
)
=
ψ
(
0
+
)
{\displaystyle \psi (0^{-})=\psi (0^{+})\;}
d
ψ
d
x
|
x
=
0
−
=
d
ψ
d
x
|
x
=
0
+
{\displaystyle \left.{d\psi \over dx}\right|_{x=0^{-}}=\left.{d\psi \over dx}\right|_{x=0^{+}}}
이 성립해야 한다. 여기서 0- 와 0+ 는 각각 좌극한과 우극한을 의미한다.
위를 정리하면 첫 번째 경계조건에서
A
+
B
=
C
+
D
{\displaystyle A+B=C+D\;}
두 번째 경계조건에서
i
k
(
A
−
B
)
=
i
k
′
(
C
−
D
)
{\displaystyle ik(A-B)=ik'(C-D)\;}
를 얻는다.
반사와 산란 [ 편집 ] 이제 이 상황을 고전역학적 관점과 비교해 볼 수 있다. 고전역학에서 퍼텐셜 단이 이렇게 있으면, 에너지가 단보다 높으면 (E > V0 단을 무시하고 통과할 것이고 에너지가 단보다 낮으면 (E < V0 ) 단에서 모든 입자가 반사될 것이다.
하지만 양자역학적 관점에서는 다른 결과를 얻는다. 입자가 단의 낮은쪽에서 오는 경우에, 즉 D = 0 인 경우, 반사되는 입자와 관련된 상수 R = B와 투과하는 입자와 관련된 상수 T = C가 A에 대해 상대적으로 얼마의 값을 가지는지 확인해보자. 편의상 A를 1로 놓고 관계식
1
+
R
=
T
{\displaystyle 1+R=T\;}
k
(
1
−
R
)
=
k
′
T
{\displaystyle k(1-R)=k'T\;}
를 풀면
R
=
k
−
k
′
k
+
k
′
{\displaystyle R={k-k' \over k+k'}}
T
=
2
k
k
+
k
′
{\displaystyle T={2k \over k+k'}}
를 얻는다. 각각의 확률흐름 을 계산해보면 x < 0 에서
j
=
ℏ
k
m
(
1
−
|
R
|
2
)
{\displaystyle j={\hbar k \over m}(1-|R|^{2})}
x > 0에서
j
=
ℏ
k
′
m
|
T
|
2
{\displaystyle j={\hbar k' \over m}|T|^{2}}
가 되고 두 흐름이 x = 0에서 같아야 하므로
ℏ
k
m
(
1
−
|
R
|
2
)
=
ℏ
k
′
m
|
T
|
2
{\displaystyle {\hbar k \over m}(1-|R|^{2})={\hbar k' \over m}|T|^{2}}
를 얻는다.
이제 여기서 반사된 흐름과 투과한 흐름의 양을 구할 수 있는데 반사된 흐름은
ℏ
k
m
|
R
|
2
=
ℏ
k
m
(
k
−
k
′
k
+
k
′
)
2
{\displaystyle {\hbar k \over m}|R|^{2}={\hbar k \over m}\left({k-k' \over k+k'}\right)^{2}}
이고, 투과한 흐름은
ℏ
k
′
m
|
T
|
2
=
ℏ
k
m
4
k
k
′
(
k
+
k
′
)
2
{\displaystyle {\hbar k' \over m}|T|^{2}={\hbar k \over m}{4kk' \over \left(k+k'\right)^{2}}}
이다. 보다시피 두 흐름의 양을 더하면 처음의 흐름의 양과 같아진다.
같이 보기 [ 편집 ]