볼록한 고른 테셀레이션의 목록

이 표는 유클리드 평면에서의 볼록한 고른 타일링(정타일링과 반정타일링)과 그 쌍대 타일링 11가지를 보여준다.

평면에서 정타일링은 세 개가 있고 반정타일링은 여덟 개가 있다. 반정타일링은 그 쌍대로 새로운 타일링을 만들고, 각각은 정다각형이 아닌 한 종류의 면에서 만들어졌다.

존 콘웨이는 아르키메데스의 다면체의 연장으로 고른 쌍대를 아르키메데스 타일링이라고 불렀다.

고른 타일링은 꼭짓점에 존재하는 면의 수열인 꼭짓점 배치를 따라 나열되었다. 예를 들어 4.8.8은 한 꼭짓점에 정사각형 하나와 정팔각형 두 개를 의미한다.

이 고른 타일링 11가지는 32가지의 다른 균일 색칠을 가진다. 균일 색칠은 점추이성이나 꼭짓점 간 변환 합동을 유지하면서 꼭짓점에 있는 동일한 다각형을 다른 색으로 칠할 수 있다(참고: 아레의 일부 타일링 그림은 색-균일하지 않을 수 있다)

볼록 고른 타일링 11가지에다가 또한 별 다각형을 사용하고 꼭짓점 배치가 원점 반전된 볼록하지 않은 타일링 14가지가 있다.

라브스 타일링[편집]

1987년에 Tilings and Patterns에서 브랑코 그린바움(Branko Grünbaum)은 점추이 타일링을 아르키메데스의 다면체의 연장으로 아르키메데스 타일링이라고 불렀다. 그 쌍대 타일링은 결정학자 프리츠 라브스(Fritz Laves)의 이름을 따 라브스 타일링이라고 불린다.^[1]^[2] 이것은 또한 슈브니코프, 알렉세이 바실레비치(Shubnikov, Alekseĭ Vasilʹevich)의 이름을 따와 슈브니코프–라브스 타일링이라고도 부른다.^[3] 존 콘웨이는 고른 쌍대를 카탈랑의 다면체의 연장선상으로 카탈랑 타일링이라고 불렀다. 콘웨이 타일링은 존슨의 다면체의 확장 개념인데, 각 면이 정다각형이며, 점추이가 아니며 평면의 면이 있으면서 볼록한 테셀레이션을 뜻한다(물론 면의 수가 유한한 것도 해당된다).

라브스 타일링의 꼭짓점은 정다각형의 중심에 가지고 있고, 변은 변을 공유하는 정다각형의 중심을 연결한다. 라브스 타일링의 타일은 planigons이라고 부른다. 이것은 정타일링 3개(정삼각형, 정사각형, 정육각형)와 정타일링이 아닌 8개를 포함한다.^[4] 각 꼭짓점은 주변에 균일하게 거리를 둔 변이 있다. planigons의 삼차원 해석은 스테레오헤드론이라고 부른다.

이 쌍대 타일링은 면 배치를 따라서 나열되어 있고, 면배치는 면의 꼭짓점에 모인 면의 개수를 의미한다. 예를 들어 V4.8.8은 한 쪽 꼭짓점에 삼각형이 네 개고, 두 꼭짓점에는 삼각형이 여덟 개가 있다는 것을 의미한다.

열한가지 planigons
삼각형				사각형			오각형			육각형
V6.6.6	V4.8.8	V4.6.12	V3.12.12	V4.4.4.4	V3.6.3.6	V3.4.6.4	V3.3.4.3.4	V3.3.3.3.6	V3.3.3.4.4	V3.3.3.3.3.3

유클리드 평면에서 볼록한 고른 타일링[편집]

All reflectional forms can be made by Wythoff constructions, represented by Wythoff symbols, or Coxeter-Dynkin diagrams, each operating upon one of three Schwarz triangle (4,4,2), (6,3,2), or (3,3,3), with symmetry represented by Coxeter groups: [4,4], [6,3], or [3^[3]]. 부풀림 같이 교대된 형태는 또한 각 시스템의 특별한 마크업으로 나타날 수 있다. O오직 고른 타일링 하나만이 위토프 과정을 통해서 구성될 수 없지만, 삼각형 타일링을 늘림으로써 얻을 수 있다. 직각 거울구조 [∞,2,∞]또한 두 쌍의 평행한 거울이 직사각형의 기본 영역을 만드는 것처럼 존재한다. I영역이 정사각형이라면 이 대칭은 대각선 거울을 추가하여 [4,4]그룹이 될 수 있다.

족:

(4,4,2), ${\tilde {BC}}_{2}$ ${\tilde {BC}}_{2}$ , [4,4] - 정사각형 타일링의 대칭
- ${\tilde {I}}_{1}^{2}$ , [∞,2,∞]
(6,3,2), ${\tilde {G}}_{2}$ ${\tilde {G}}_{2}$ , [6,3] - 정육각형 타일링과 정삼각형 정타일링의 대칭
- (3,3,3), ${\tilde {A}}_{2}$ , [3^[3]]

[4,4] 그룹[편집]

고른 타일링 (플라톤과 아르키메데스)	꼭짓점 도형과 쌍대 면 위토프 기호 대칭군 콕서터 다이어그램	쌍대-고른 타일링 (라브스 또는 카탈랑 타일링)
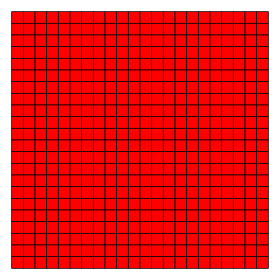정사각형 타일링 (quadrille)	4.4.4.4 (or 4⁴) 4 \| 2 4 p4m, [4,4], (*442)	자기쌍대 (quadrille)
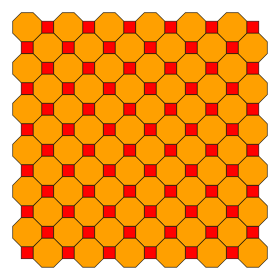깎은 정사각형 타일링 (truncated quadrille)	4.8.8 2 \| 4 4 4 4 2 \| p4m, [4,4], (*442) or	Tetrakis square tiling (kisquadrille)
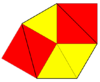부풀린 사각형 타일링 (snub quadrille)	3.3.4.3.4 \| 4 4 2 p4g, [4⁺,4], (4*2) or	카이로 오각형 타일링 (4-fold pentille)

. [6,3] 그룹[편집]

플라톤과 아르키메데스 타일링	꼭짓점 도형과 쌍대 면 위토프 기호 대칭군 콕서터 다이어그램	쌍대 라브스 타일링
정육각형 타일링 (hextille)	6.6.6 (or 6³) 3 \| 6 2 2 6 \| 3 3 3 3 \| p6m, [6,3], (*632)	정삼각형 타일링 (deltille)
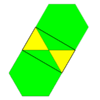삼육각형 타일링 (hexadeltille)	(3.6)² 2 \| 6 3 3 3 \| 3 p6m, [6,3], (*632) =	Rhombille tiling (rhombille)
깎은 정육각형 타일링 (truncated hextille)	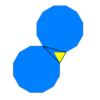3.12.12 2 3 \| 6 p6m, [6,3], (*632)	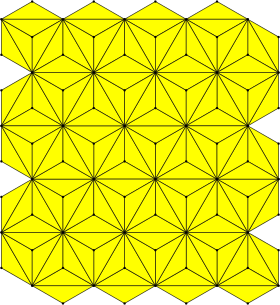Triakis triangular tiling (kisdeltille)
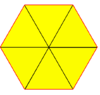정삼각형 타일링 (deltille)	3.3.3.3.3.3 (or 3⁶) 6 \| 3 2 3 \| 3 3 \| 3 3 3 p6m, [6,3], (*632) =	정육각형 타일링 (hextille)
마름모삼육각형 타일링 (rhombihexadeltille)	3.4.6.4 3 \| 6 2 p6m, [6,3], (*632)	Deltoidal trihexagonal tiling (tetrille)
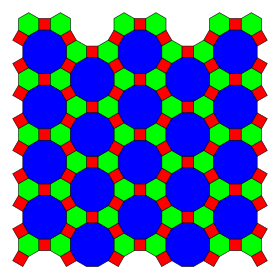깎은 삼육각형 타일링 (truncated hexadeltille)	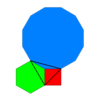4.6.12 2 6 3 \| p6m, [6,3], (*632)	Kisrhombille tiling (kisrhombille)
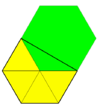부풀린 삼육각형 타일링 (snub hextille)	3.3.3.3.6 \| 6 3 2 p6, [6,3]⁺, (632)	Floret pentagonal tiling (6-fold pentille)

위토프가 아닌 고른 타일링[편집]

플라톤과 아르키메데스 타일링	꼭짓점 도형과 쌍대 면 위토프 기호 대칭군 콕서터 다이어그램	쌍대 라브스 타일링
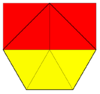늘린 삼각형 타일링 (isosnub quadrille)	3.3.3.4.4 2 \| 2 (2 2) cmm, [∞,2⁺,∞], (2*22)	Prismatic pentagonal tiling (iso(4-)pentille)

균일 색칠[편집]

고른 타일링 11가지에 대한 균일 색칠은 32가지가 있다:

정삼각형 타일링 - 9 균일 색칠, 4 위토프, 5 비-위토프
정사각형 타일링 - 9 색칠: 7 위토프, 2 비-위토프
정육각형 타일링 - 3 색칠, 모두 위토프
삼육각형 타일링 - 2 색칠, 둘 다 위토프
부풀린 정사각형 타일링 - 2 색칠, 둘 다 교대된 위토프
깎은 정사각형 타일링 - 2 색칠, 둘 다 위토프
깎은 정육각형 타일링- 1 색칠, 위토프
마름모삼육각형 타일링 - 1 색칠, 위토프
깎은 삼육각형 타일링- 1 색칠, 위토프
부풀린 정육각형 타일링- 1 색칠, 교대된 위토프
비틀어 늘린 사각형 타일링- 3 색칠, 비-위토프

같이 보기[편집]

고른 타일링
볼록한 고른 벌집- 28가지 고른 3차원 테셀레이션, 볼록 유클리드 평면 타일링과 평행선상의 구성.
쌍곡면에서의 고른 타일링
여과 역치

참조[편집]

↑ Grünbaum, Branko; Shephard, G. C. (1987). 《Tilings and Patterns》. W. H. Freeman and Company. 59, 96쪽. ISBN 0-7167-1193-1. CS1 관리 - 여러 이름 (링크)
↑ The Symmetries of things, Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Euclidean Plane Tessellations, p. 288
↑ Encyclopaedia of Mathematics: Orbit - Rayleigh Equation edited by Michiel Hazewinkel, 1991
↑ Ivanov, A. B. (2001). “Planigon”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. ISBN 978-1-55608-010-4.

추가 자료[편집]

John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 [1] (Chapter 19, Archimedean tilings, table 19.1, Chapter 21, Naming Archimedean and Catalan polyhedra and tilings, p288 table).
H.S.M. Coxeter, M.S. Longuet-Higgins, J.C.P. Miller, Uniform polyhedra, Phil. Trans. 1954, 246 A, 401–50.
틀:The Geometrical Foundation of Natural Structure (book) (Section 2–3 Circle packings, plane tessellations, and networks, pp 34–40).
Asaro, et. al. "Uniform edge-c-colorings of the Archimedean Tilings", [2].
Grünbaum, Branko & Shepard, Geoffrey (Nov. 1977). "Tilings by Regular polygons", Vol. 50, No. 5.
Dale Seymour and Jill Britton, Introduction to Tessellations, 1989, ISBN 978-0866514613, pp. 50–57, 71-74

외부 링크[편집]

Weisstein, Eric Wolfgang. “Uniform tessellation”. 《Wolfram MathWorld》 (영어). Wolfram Research.
Uniform Tessellations on the Euclid plane
Tessellations of the Plane
David Bailey's World of Tessellations
k-uniform tilings
n-uniform tilings

[1] Grünbaum, Branko; Shephard, G. C. (1987). 《Tilings and Patterns》. W. H. Freeman and Company. 59, 96쪽. ISBN 0-7167-1193-1. CS1 관리 - 여러 이름 (링크)

[2] The Symmetries of things, Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Euclidean Plane Tessellations, p. 288

[3] Encyclopaedia of Mathematics: Orbit - Rayleigh Equation edited by Michiel Hazewinkel, 1991

[4] Ivanov, A. B. (2001). “Planigon”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. ISBN 978-1-55608-010-4.

[1]

[2]

[3]

[4]