말뚝

말뚝(pile)은 땅에 박기 위하여 한쪽 끝을 삐죽하게 만든 기둥이나 몽둥이 모양의 물건 또는 그것을 땅에 박아 놓은 것을 가리키는 단어이다. 말뚝은 건물이 가라앉거나 무너지지 않게 하는 역할을 한다. 건물의 기초가 땅 위 상층부를 지지하기에 너무 약하면 말뚝을 사용해서 구조물의 무게를 지하의 단단한 흙이나 암반으로 전달하면 된다. 마천루와 같은 고층 건물의 기초는 지하 60m까지 말뚝을 박는 경우도 있다.

분류

• 기성말뚝 : 공장 제작, 현장으로 운반하여 설치되는 말뚝
• 현장말뚝 : 현장에서 땅에 구멍을 뚫고 철근과 콘크리트를 채워 제작하는 말뚝

기성말뚝

• 원심력 철근콘크리트 말뚝
  • 중간정도 굳은 지층에 불리
  • 말뚝 이음 신뢰성 낮음.
  • 항타 시 편심 타격으로 두부 손상 가능.
  • 타격 해머 무게, 타격 에너지 과다로 두부 손상 가능.
• 프리스트레스트 콘크리트 말뚝
  • 말뚝 이음 신뢰성 높음
  • 프리스트레스에 의해 인장파괴 일어나지 않음.
  • 대구경 제조 가능.

강관말뚝

• 강관말뚝
  • 굳은 지층 관통 가능.
  • 이음 신뢰성 높음.
  • 강도 큼
  • 대구경 제조 가능.
  • 부식 대책으로 두꺼운 강관을 쓰거나, 표면 도료칠, 전기 방식을 할 수 있음.

공법

기성말뚝 공법

• 매입공법
  • 압입공법
  • pre boring
  • SIP(Soil cement Injected Precast pile) : 무소음, 무진동 공법.
• 타입공법
  • 타격공법
    • 디젤 해머 : 타격력 우수. 기동성 좋음.
  • 진동공법
    • 진동 해머 : 말뚝 인발 가능. 무소음. 시공 속도 빠름.

• 

  디젤 해머

• 

  진동해머(vibro hammer)

현장말뚝 공법

• 기계굴착 공법
  • benoto 공법(all casing)
  • Earth drill 공법(Calwelde drill)
  • RCD 공법(Reverse Circulation Drill)

• 관입공법
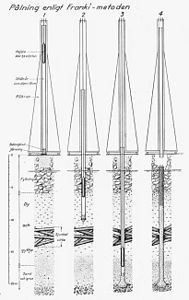
  • Franky pile
  • Raymond pile
  • Pedestal pile

• 

  RCD

• 

  Franky pile

• 기타
  • CIP(Cast In Place pile)
  • MIP(Mixed In Place pile)
  • PIP(Packed In Place pile)

말뚝에 작용하는 하중

 이 부분의 본문은 기초 § 말뚝에 작용하는 하중입니다.

말뚝에 작용하는 하중은 축하중과 수평하중이 있다. n개의 말뚝으로 이루어진 말뚝기초에서 말뚝 하나가 받는 축하중은 다음 식으로 구한다. 축하중을 계산할 때는 편심하중이나 수평하중으로 인해 말뚝기초 상단의 확대기초(파일 캡)에 모멘트가 작용하기 때문에 각 말뚝이 받는 축하중은 단순히 전체 연직하중 P를 말뚝 개수 n으로 나눈 것이 아니다. i번째 말뚝이 받는 축하중을 P_i라 할 때,

$P_{i}={\frac {P}{n}}\pm {\frac {M_{y}}{\Sigma {x_{i}}^{2}}}x_{i}\pm {\frac {M_{x}}{\Sigma {y_{i}}^{2}}}y_{i}$

P : 연직하중의 합력(사하중 + 활하중)

M_x, M_y : x축, y축에 대한 모멘트(편심하중에 의한 모멘트는 각 축에서 편심하중 P까지의 수직거리를 곱해준다)

x_i, y_i : i번째 말뚝에서 x, y축까지의 거리

각 말뚝이 받는 수평하중은 기초에 작용하는 수평하중 H를 말뚝 개수 n으로 나눠주면 된다.

$H_{i}={\frac {H}{n}}$

상부구조물에 작용하는 수평하중이 말뚝에 전달되는 경우는 주동말뚝이라고 하고, 말뚝 주변 지반 변형이 말뚝에 하중으로 작용되는 경우는 수동말뚝이라고 한다.

지지력

말뚝의 축방향 극한 지지력 Q_u는 말뚝 극한 선단지지력 Q_p와 극한주면마찰저항력 Q_s의 합과 같다.

$Q_{u}=Q_{p}+Q_{s}$

말뚝의 지지력을 구하는 공식에는 동역학적 지지력 공식과 정역학적 지지력 공식이 있다. 사질토 지반에는 동역학적 지지력 공식이 적합하고, 점성토 지반에는 정역학적 지지력 공식을 사용한다. 공식 외에 항타분석기(PDA; Pile Driving Analyzer)를 통해 지지력을 구하는 방법도 있다.

동역학적 지지력 공식

동역학적 지지력 공식은 엔지니어링 뉴스(Engineering News) 공식, 샌더(Sander) 공식, Hiley 공식, Weisbach 공식이 있다.

엔지니어링 뉴스(Engineering News) 공식

해머의 중량 $W_{H}$, 해머 낙하고 H(cm), 타격 당 말뚝의 평균 관입량 S(cm), 안전율 F_s라 할 때

극한 지지력 $R_{u}={\frac {W_{H}\cdot H}{S+C}}$

허용 지지력 $R_{a}={\frac {R_{u}}{F_{s}}}={\frac {W_{H}\cdot H}{6(S+C)}}$

• C : 손실상수
  • 단동식 증기 해머 0.254cm
  • drop hammer 2.54cm

샌더(Sander) 공식

극한 지지력 $R_{u}={\frac {W_{H}\cdot H}{S}}$

허용 지지력 $R_{a}={\frac {R_{u}}{F_{s}}}={\frac {W_{H}\cdot H}{8S}}$

정역학적 지지력 공식

 이 부분의 본문은 기초 § 정역학적 지지력 공식입니다.

정역학적 지지력 공식에는 Dörr 공식, 테르자기(Terzaghi) 공식, Meyerhof 공식, Dunham 공식이 있다.

극한 선단지지력

말뚝의 극한 선단지지력 Q_p는 단위면적당 극한선단지지력(단위선단지지력)을 q_p, 선단부 내부가 흙으로 완전히 채워졌다고 가정하는 경우의 말뚝 저부 면적을 A_b라 할 때 다음과 같다.

$Q_{p}=q_{p}A_{b}$

단위 선단지지력 q_p는 얕은 기초의 극한 지지력 공식 $q_{u}=cN_{c}^{*}+qN_{q}^{*}+{\frac {1}{2}}\gamma _{1}BN_{\gamma }^{*}$에서 기초 단변 길이 B를 말뚝 직경 D로 바꾼 식을 사용한다. *가 붙은 지지력 계수들은 형상계수, 깊이계수, 경사하중 계수를 모두 고려한 지지력 계수임을 의미한다. 말뚝 직경 D는 크지 않으므로 세 번째 항을 무시할 수 있고 q는 유효상재압력 σ_v'을 사용하므로 식은 다음과 같이 된다.

$q_{p}=cN_{c}^{*}+\sigma _{v}'N_{q}^{*}$

사질토인 경우, c=0이므로 단위선단지지력 $q_{p}=\sigma _{v}'N_{q}^{*}$이다. 말뚝이 타입 말뚝인지 현장 타설 말뚝인지에 따라 N_q^*가 달라진다. 단위선단지지력은 말뚝 깊이가 깊어질수록 σ_v'의 증가에 따라 커지나, 말뚝 직경 D의 20배까지의 한계깊이 이하에서는 일정하다. 즉 $\sigma _{v}'\leq \gamma '(20D)$를 한계로 한다.

포화된 점토에서 비배수 조건인 경우 $\phi _{u}=0$이므로 $q_{p}=c_{u}N_{c}^{*}$이다. c_u는 점토의 비배수 전단강도이다. 관입비가 4 이상인 정방 기초 혹은 원형 기초는 N_c^*=9이다. 따라서 $q_{p}=9c_{u}$이다.

극한 주면마찰저항력

말뚝의 주면마찰저항력 Q_s는 다음 식으로 나타난다.

$Q_{s}=\Sigma p\Delta L\cdot f_{s}$

p : 말뚝 단면의 윤변

ΔL : p와 f_s가 일정한 곳에서 말뚝의 길이

f_s : 깊이 z에서의 단위 주면마찰저항력

f_s는 흙과 구조체의 전단강도 식으로, 다음과 같이 구한다.

${\begin{aligned}f_{s}&=c_{a}+{\sigma _{n}}'\tan \delta \\&=c_{a}+K_{s}{\sigma _{v}}'\tan \delta \\\end{aligned}}$

• c_a : 말뚝과 주변 흙 사이의 부착력
• δ : 말뚝과 주변 흙 사이의 벽면마찰각
• K_s : 말뚝면에 작용하는 토압계수

사질토의 단위 주면마찰저항력은 c_a=0이므로 $f_{s}=K_{s}{\sigma _{v}}'\tan \delta$이다. 선단지지력과 마찬가지로 깊이가 깊어질수록 주면마찰저항력이 커지다가 말뚝 직경 D의 20배까지의 한계깊이 이하에서는 일정해진다. 즉 ${\sigma _{v}}'\leq {\gamma }'(20D)$를 한계로 한다. 토압계수 K_s는 말뚝이 타입 말뚝인지 굴착 말뚝인지에 따라 달라진다. 벽면마찰각 δ는 말뚝의 재료에 따라 달라진다.

점토의 단위 주면마찰저항력은 전응력 해석법인 α계수법과 유효응력 해석법인 β계수법을 통해 구한다.

α계수법은 비배수 전단강도 c_u를 사용하며, Φ_u=0이므로 δ=0이 되어 $f_{s}=c_{a}=\alpha \cdot c_{u}$ 식으로 점토의 단위 주면마찰저항력을 구한다. 여기서 α는 부착력 계수이다.

β계수법은 포화 점토지반에 말뚝을 타입하고 지반에 과잉간극수압이 발생하며 점토가 교란되었다가 과잉간극수압이 소산된 후, 재성형된 점토에 대해 유효응력을 이용하여 해석하는 방법이다. 저항력은 다음 식으로 구한다.

${\begin{aligned}f_{s}&={c_{r}}'+{\sigma _{n}}'\tan {\phi _{r}}'\\&={c_{r}}'+K_{s}{\sigma _{v}}'\tan {\phi _{r}}'\\\end{aligned}}$

• c_r' : 재성형된 점토의 점착력
• K_s : 토압계수(보통 정지토압계수)$={\begin{cases}1-\sin {\phi _{r}}'&{\text{정 규 압 밀 점 토 인 경 우}}\\(1-\sin {\phi _{r}}'){\sqrt {OCR}}&{\text{과 압 밀 점 토 인 경 우}}\end{cases}}$
• Φ_r' : 재성형된 점토의 내부마찰각

재성형된 점토의 점착력${c_{r}}'\approx 0$이므로 식은 다음처럼 간략화된다.

$f_{s}=K_{s}{\sigma _{v}}'\tan {\phi _{r}}'$

여기서 $\beta =K_{s}\tan {\phi _{r}}'$이므로 $f_{s}=\beta {\sigma _{v}}'$이다.

항타분석기 사용

항타분석기를 사용하면 시공관리 상 다음의 이점이 있다.

• 항타와 동시에 항타기 효율, 적합성 판단 가능.
• 빠른 계측이 가능.

지지력 저하

기성말뚝은 다음 원인으로 지지력 저하가 발생할 수 있다.

• 말뚝 이음
• 말뚝 침하

군항의 지지력

하나의 말뚝을 단항이라 한다면, 여러 개의 말뚝은 군항 또는 무리말뚝(group pile)이라 한다. 일반적으로 말뚝은 여러개를 박는다. 말뚝이 여러 개 박혀있을 때 지지력을 감소시킬지(군항으로 볼지) 감소시키지 않을지(단항의 집합으로 볼지)는 아래 식으로 정한다.

$S<1.5{\sqrt {rL}}$

• r : 말뚝 반경

• L : 말뚝 길이

군항의 허용 지지력 $R_{ag}$은 단순히 단항의 허용 지지력$R_{a}$에 말뚝 개수 N을 곱한 것이 아니라, 말뚝부터의 지중 응력이 중복되기 때문에 말뚝 한 개당 지지력이 약화되므로, 별도의 식을 이용해야 한다. 무리말뚝의 효율을 E라고 한다면 다음과 같이 구할 수 있다.

$R_{ag}=E\Sigma R_{a}$

마찰말뚝의 경우 극한지지력을 이용하여 식을 나타낸다면

$Q_{ug}=E\Sigma Q_{u}$

단일 말뚝의 주면 마찰저항력 Q_u는 p가 윤변, $f_{s(avg)}$가 평균 단위주면마찰저항력이라 할 때,

$Q_{u}=pLf_{s(avg)}$

블록으로 작용하는 경우 주면마찰저항력 Q_ug는 m이 말뚝의 열수, n은 한개 열의 말뚝 수라 할 때,

${\begin{aligned}Q_{ug}&=p_{g}Lf_{s(avg)}\\&=\left[2(m-1+n-1)S+8{\frac {D}{2}}\right]Lf_{s(avg)}\\&=[2(m+n-2)S+4D]Lf_{s(avg)}\end{aligned}}$

${\begin{aligned}\therefore E&={\frac {Q_{ug}}{\Sigma Q_{u}}}={\frac {[2(m+n-2)S+4D]Lf_{s(avg)}}{mnpLf_{s(avg)}}}\\&={\frac {2(m+n-2)S+4D}{mnp}}\end{aligned}}$

군항의 효율 E는 Converse-Labarre의 저감식을 통해서도 계산할 수 있다.

$E=1-\phi {\frac {(m-1)n+(n-1)m}{90mn}}$

$\phi =tan^{-1}{\frac {D}{S}}$

D : 말뚝의 직경, S : 말뚝 중심간의 간격

사질토에 타입된 마찰말뚝이나, 암반에 근입된 마찰말뚝은 효율 E를 1로 한다. 반면 사질토나 점토에 매입된 말뚝은 위 식에 따라 무리말뚝의 효율이 달라지게 된다. 특히 점토지반에 근입된 무리말뚝의 극한지지력 Q_ug는 다음 두 값 중 작은 값을 선택한다. 여기서 c_u(b)는 말뚝 저면의 점토층 비배수전단강도이다.

• 단일말뚝의 극한지지력 Q_u총합$(\Sigma Q_{u}=mn(Q_{p}+Q_{s})=mn(q_{p}A_{b}+\Sigma f_{s}A_{s}=mn(9c_{u(b)}A_{b}+\Sigma \alpha c_{u}pL)$
• 무리말뚝의 영역을 블록으로 봤을 때의 극한지지력$(Q_{ug}=Q_{pg}+Q_{sg}=q_{p}A_{b}+\Sigma c_{u}p_{g}\Delta L=c_{u(b)}N_{c}^{*}(B_{g}\cdot L_{g})+\Sigma c_{u}\cdot 2(B_{g}+L_{g})\Delta L)$

부마찰력

말뚝 기초는 선단 지지력과 주면 마찰력에 의해 상부 하중을 지반에 전달한다. 그러나 주변 지반이 말뚝보다 더 많이 침하하여 상향으로 작용해야 하는 주면 마찰력이 아래쪽으로 작용하는 경우가 생기는데 이때의 마찰력을 부마찰력(negative friction; $R_{nf}$) 또는 부주면마찰력이라 한다. 부마찰력은 말뚝을 아래쪽으로 끌어내린다.

$R_{nf}=U\cdot l_{c}\cdot f_{s}$

• U : 말뚝의 주변장$(U=\pi D)$ (D : 말뚝 직경)
• $l_{c}$ : 관입 깊이
• $f_{s}$ : 말뚝의 평균 마찰력 또는 일축 압축 강도의 절반값$\left(f_{s}={\frac {q_{u}}{2}}\right)$

부마찰력의 특징

• 부마찰력 발생 시 말뚝의 지지력은 감소
• 연약한 점토에서 부마찰력은 상대 변위의 속도가 느릴수록 작고, 빠를수록 크다.

부마찰력 발생 경우

• 압밀층을 관통하여 견고한 지반에 말뚝을 박는 경우
• 연약 지반을 관통하여 말뚝을 박고 그 위에 성토하는 경우
• 연약 지반을 관통하여 견고한 지반에 말뚝을 박는 경우
• 지하수위 하강
• 말뚝 항타 후 지반의 간극수압이 상승하는데(과잉간극수압 발생) 나중에 과잉간극수압이 다시 떨어져 원래대로 돌아오는 경우

부마찰력 방지책

• 표면적 큰 말뚝 사용(H형강 말뚝)
• 말뚝 표면 역청재 도포
• 말뚝 직경보다 크게 pre boring

같이 보기

• 기초공학

참고 문헌

• 이인모 (2015). 《기초공학의 원리》. 씨아이알. ISBN 979-11-5610-063-8. 
• 권호진; 김동수; 박준범; 정성교 (2015). 《기초공학》 2판. 구미서관. ISBN 978-89-8225-5854. 
• 이 문서에는 다음커뮤니케이션(현 카카오)에서 GFDL 또는 CC-SA 라이선스로 배포한 글로벌 세계대백과사전의 내용을 기초로 작성된 글이 포함되어 있습니다.
• 임진근 외 (2015). 《토목기사 필기 토질 및 기초》. 성안당. 
• 박영태 (2019). 《토목기사 실기》. 세진사. 
• Das. 《기초공학》 5판. 인터비젼. 

외부 링크

• 대한전문건설신문 - 고강도콘크리트(PHC) 말뚝 연결방식 분쟁, 볼트체결 신기술 일단 판정승
• 대흥기초건설 - 한림 ~ 생림간 도로현장 D1000 BG공법