아폴로니오스의 정리

초등 기하학에서 아폴로니오스의 정리(Apollonius' theorem)는 삼각형의 각 변들간의 관계를 설명한 정리이다. 중선정리라는 이름으로도 널리 알려져 있고, 대한민국에서는 흔히 파푸스의 중선정리(Pappus's centroid theorem)라는 이름으로 알려져 있으나 이 정리에 파푸스(Pappus)의 이름을 붙여 부르는 예는 대한민국과 일본 이외에는 찾을 수 없다. '아폴로니오스'라는 이름은 고대 그리스의 수학자인 페르게의 아폴로니오스의 이름을 딴 것이다.

정리의 서술

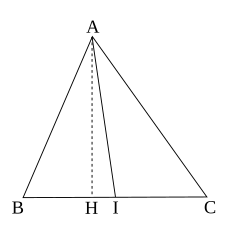
그림에서 $BI = IC$일 때, 선분 $AI$는 중선(Median)이 되고, 다음의 관계가 성립한다.

$AB^2 + AC^2 = 2(BI^2 + AI^2) \,$

특히, $AB = AC$가 성립할 경우, 피타고라스의 정리가 된다. 즉,

$AI^2 + BI^2 = AB^2 (= AC^2)\,$

이 정리는 스튜어트 정리에서 $BI = IC$를 가정할 때와 동일하므로 스튜어트 정리의 특수한 형태가 된다.

같이보기

• 스튜어트 정리

바깥고리

• planetmath.org의 Apollonius theorem항목