르장드르의 구면삼각형 정리

기하학에서 르장드르의 구면삼각형 정리(Legendre's theorem on spherical triangles)의 구형삼각형(구면삼각형)에 대한 정리는 아드리앵마리 르장드르(Adrien-Marie Legendre)의 이름을 따서 명명했다.

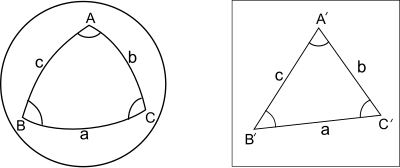
ABC를 작은 변 a , b , c 가있는 구면의 구형 삼각형이라고한다면, A' , B' , C'를 같은면이있는 평면 삼각형이라고 비교할 수 있다. 그렇다면 구면삼각형의 각도가 평면 삼각형의 대응 각도를 구면과잉(spherical excess)의 약 1/3만큼 초과한다 (구형과잉 또는 구면과잉은 세 각도의 합이 π를 초과하는 양)

이 정리는 1800년경부터 20세기 중반까지 전통적 GPS 측지 측량 결과를 계산할 때 어려운 수치 작업을 간소화하는 데 매우 중요했다.

이 정리는 르장드르(Legendre,1787)가 미터(DTambambre , 1798)의 정의에 사용된 프랑스원정대의 자오선 측정보고서(French Geodesic Mission)를 보완하는 증거(1798 )를 제공 한 것으로 명시되었다. 르장드르는 그가 자신의 제공에도 불구하고 정리의 창시자라고 주장하지 않았다. 트로프케(Tropfke ,1903)는 그 방법이 당시 측량사들에 의해 일반적으로 사용되었고 페루 자오선 호 계산을 위해 라 콘다민 (La Condamine)이 1740년에 이미 사용했을지도 모른다고 언급했다.

알버트 지라드(Albert Girard)의 지라드의 정리(Girard's theorem)는 삼각형 E 의 구형 과잉(spherical excess)이 영역Δ와 동일하므로 르장드르의 정리(Legendre's theorem)는 다음과 같이 쓰여질 수 있다고 기술한다.

${\begin{aligned}A-A'\;\approx \;B-B'\;\approx \;C-C'\;\approx \;{\frac {1}{3}}E\;=\;{\frac {1}{3}}\Delta ,\qquad a,\;b,\;c\,\ll \,1\end{aligned}}$

작은 삼각형의 과잉영역은 매우 작다. 예를 들어 반경이 6371km 인 구형 지구상에 60km의 변이있는 정삼각형의 구형 삼각형을 생각해보면, 측면은 60/6371 = .0094 또는 약 10^-2 라디안 (중심에서 0.57°의 각도를 나타냄)의 각도 거리에 해당한다. 그러한 작은 삼각형의 면적은 같은면을 가진 평면 정삼각형의 면적으로 잘 근사화된다 : 1/2a² sin (π/3) = 0.0000433 라디안 (8.9 "에 해당).

삼각형의 변이 180km를 초과 할 때, 초과분이 약 80"인 경우, 영역과 각도의 차이는 측의 4차항의 항으로 0.01"이하로 정정되어야한다.

${\begin{aligned}\Delta &=\Delta '\left(1+{\frac {a^{2}+b^{2}+c^{2}}{24}}\right),\\A&=A'+{\frac {\Delta }{3}}+{\frac {\Delta }{180}}\left(-2a^{2}+b^{2}+c^{2}\right),\\B&=B'+{\frac {\Delta }{3}}+{\frac {\Delta }{180}}\left({\quad a^{2}-2b^{2}+c^{2}}\right),\\C&=C'+{\frac {\Delta }{3}}+{\frac {\Delta }{180}}\left({\quad a^{2}+b^{2}-2c^{2}}\right)\end{aligned}}$

(Δ'는 평면 삼각형의 면적)이 결과는 Buzengeiger (1818)에 의해 입증되었다. 확장 된 증거는 Osborne (2013) (부록 D13)에서 찾을 수 있다. 다른 결과는 Nádeník (2004)에 의해 조사되었다.

a , b , c 가 진정한 길이를 주 곡률 반경 ( Osborne (2013) 5 장 참조)의 곱의 제곱근으로 나누어서 정점의 중간 위도에서 정리하면 타원체로 확장될수있다 (구형 반지름 대신). 가우스(1828 , Art. 26-28)는보다 정확한 공식을 제시했다.

같이 보기

• 구면삼각법

참고

• Buzengeiger, Karl Heribert Ignatz (1818), “Vergleichung zweier kleiner Dreiecke von gleichen Seiten, wovon das eine sphärisch, das andere eben ist”, 《Zeitschrift für Astronomie und verwandte Wissenschaften》 6: 264–270 
• Clarke, Alexander Ross (1880), 《Geodesy》, Clarendon Press. Republished at Forgotten Books. 
• Gauss, C. F. (1902) [1828]. 《General Investigations of Curved Surfaces of 1827 and 1825》. Princeton Univ. Lib. English translation of Disquisitiones generales circa superficies curvas (Dieterich, Göttingen, 1828). 
• Legendre, Adrien-Marie (1787), 《Mémoire sur les opérations trigonométriques, dont les résultats dépendant de la figure de la Terre》, Article  VI [1], 7쪽 
• Legendre, Adrien-Marie (1798), 《Méthode pour déterminer la longueur exacte du quart du méridien d’après les observations faites pour la mesure de l’arc compris entre Dunkerque et Barcelone》, 12–14 (Note III [2])쪽 
• Nádeník, Zbynek (2004), 《Legendre theorem on spherical triangles》 (PDF), 2014년 1월 16일에 원본 문서 (PDF)에서 보존된 문서 
• Osborne, Peter (2013), 《The Mercator Projections》, 2013년 9월 24일에 원본 문서에서 보존된 문서 
• Tropfke, Johannes (1903), 《Geschichte der Elementar-Mathematik (Volume 2).》, Verlag von Veit, 295쪽 
• (Spherical Trigonometry, I. Todhunter)https://www.gutenberg.org/files/19770/19770-pdf.pdf