PID 제어기
이 문서의 내용은 출처가 분명하지 않습니다. (2010년 10월) |

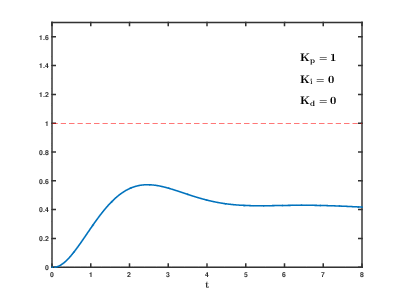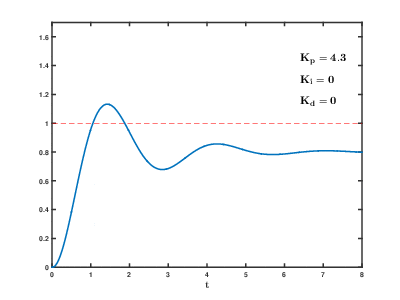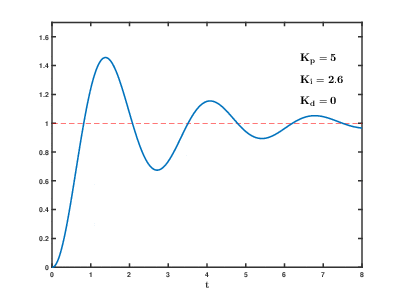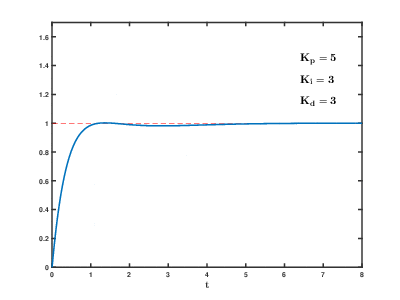
비례-적분-미분 제어기(Proportional-Integral-Differential controller) 또는 PID 제어(PID control)는 실제 응용분야에서 가장 많이 사용되는 대표적인 형태의 제어기법이다. PID 제어기는 기본적으로 피드백(feedback)제어기의 형태를 가지고 있으며, 제어하고자 하는 대상의 출력값(output)을 측정하여 이를 원하고자 하는 참조값(reference value) 혹은 설정값(Set Point)과 비교하여 오차(error)를 계산하고, 이 오차값을 이용하여 제어에 필요한 제어값을 계산하는 구조로 되어 있다.
표준적인 형태의 PID 제어기는 아래의 식과 같이 세개의 항을 더하여 제어값(MV : Manipulated Variable)을 계산하도록 구성이 되어 있다.
이 항들은 각각 오차값, 오차값의 적분(integral), 오차값의 미분(derivative)에 비례하기 때문에 비례-적분-미분 제어기 (Proportional–Integral–Derivative controller)라는 명칭을 가진다. 이 세개의 항들의 직관적인 의미는 다음과 같다.
- 비례항 : 현재 상태에서의 오차값의 크기에 비례한 제어작용을 한다.
- 적분항 : 정상상태(steady-state) 오차를 없애는 작용을 한다.
- 미분항 : 출력값의 급격한 변화에 제동을 걸어 오버슛(overshoot)을 줄이고 안정성(stability)을 향상시킨다.
PID 제어기는 위와 같은 표준식의 형태로 사용하기도 하지만, 경우에 따라서는 약간 변형된 형태로 사용하는 경우도 많다. 예를 들어, 비례항만을 가지거나, 혹은 비례-적분, 비례-미분항만을 가진 제어기의 형태로 단순화하여 사용하기도 하는데, 이때는 각각 P, PI, PD 제어기라 불린다.
한편, 계산된 제어값이 실제 구동기(actuator)가 작용할 수 있는 값의 한계보다 커서 구동기의 포화(saturation)가 발생하게 되는 경우, 오차의 적분값이 큰 값으로 누적되게 되어서, 정작 출력값이 설정값에 가까워지게 되었을 때, 제어값이 작아져야 함에도 불구하고 계속 큰 값을 출력하게 되어 시스템이 설정값에 도달하는 데 오랜 시간이 걸리게 되는 경우가 있는데, 이를 적분기의 와인드업이라고 한다. 이를 방지하기 위해서는 적절한 안티 와인드업(Anti-windup) 기법을 이용하여 PID 제어기를 보완해야 한다.
위의 식에서 제어 파라메터 를 이득값 혹은 게인(gain)이라고 하고, 적절한 이득 값을 수학적 혹은 실험적/경험적 방법을 통해 계산하는 과정을 튜닝(tuning)이라고 한다. PID 제어기의 튜닝에는 여러 가지 방법들이 있는데, 그중 가장 널리 알려진 것으로는 지글러-니콜스 방법이 있다.
같이 보기[편집]
참고[편집]
- (카네기 멜런 대학교 - PID 시뮬레이션)https://www.cs.cmu.edu/afs/cs/academic/class/15883-f15/lectures/cerebellum-controller/pid.xls
- ((주)승전 - 제 8 장 PID제어기 설계법)http://www.icdevice.com/techinfo/FA_Power_Up/phpQUDXf0/sys_chap8.pdf[깨진 링크(과거 내용 찾기)]
- (인포라드(주) - PID Control 이란 무엇일까요?)https://www.inforad.co.kr/single-post/2016/12/08/pid-control


