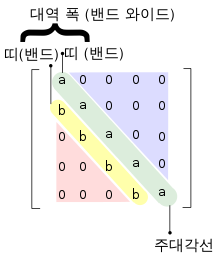
띠행렬 행렬론 에서 띠행렬 (-行列, 영어 : band matrix )은 모든 0이 아닌 성분이 주대각선 주변에 집중된 희소 행렬 이다.[1]
환
R
{\displaystyle R}
m
×
n
{\displaystyle m\times n}
M
{\displaystyle M}
하대역폭 (下帶域幅, 영어 : lower bandwidth )은 다음 조건을 만족시키는 음이 아닌 정수
p
{\displaystyle p}
[1] :15, §1.2.1
만약
i
>
j
+
p
{\displaystyle i>j+p}
M
i
j
=
0
{\displaystyle M_{ij}=0}
환
R
{\displaystyle R}
m
×
n
{\displaystyle m\times n}
M
{\displaystyle M}
상대역폭 (上帶域幅, 영어 : upper bandwidth )은 다음 조건을 만족시키는 음이 아닌 정수
p
{\displaystyle p}
[1] :15, §1.2.1
만약
j
>
i
+
p
{\displaystyle j>i+p}
M
i
j
=
0
{\displaystyle M_{ij}=0}
환
R
{\displaystyle R}
m
×
n
{\displaystyle m\times n}
M
{\displaystyle M}
대역폭 (帶域幅, 영어 : bandwidth )은
M
{\displaystyle M}
k
{\displaystyle k}
만약
|
i
−
j
|
>
k
{\displaystyle |i-j|>k}
M
i
j
=
0
{\displaystyle M_{ij}=0}
예를 들어, 하대역폭 2 및 상대역폭 1를 갖는 9×4 띠행렬은 다음과 같은 꼴이다 (
M
i
j
∈
R
{\displaystyle M_{ij}\in R}
(
M
11
M
12
0
0
M
21
M
22
M
23
0
M
31
M
32
M
33
M
34
0
M
42
M
43
M
44
0
0
M
53
M
54
0
0
0
M
64
0
0
0
0
0
0
0
0
0
0
0
0
)
{\displaystyle {\begin{pmatrix}M_{11}&M_{12}&0&0\\M_{21}&M_{22}&M_{23}&0\\M_{31}&M_{32}&M_{33}&M_{34}\\0&M_{42}&M_{43}&M_{44}\\0&0&M_{53}&M_{54}\\0&0&0&M_{64}\\0&0&0&0\\0&0&0&0\\0&0&0&0\end{pmatrix}}}
특수한 하대역폭·상대역폭을 갖는 띠행렬에는 다음과 같은 이름이 붙는다.[1] :15, §1.2.1, Table 1.2.1
하대역폭
상대역폭
이름
0
0
대각 행렬
0
1
상쌍대각 행렬(영어 : upper bidiagonal matrix )
1
0
하쌍대각 행렬(영어 : lower bidiagonal matrix )
1
1
3중 대각 행렬(영어 : tridiagonal matrix )
2
2
5중 대각 행렬(영어 : pentadiagonal matrix )
3
3
7중 대각 행렬(영어 : heptadiagonal matrix )
0
n
−
1
{\displaystyle n-1}
상삼각 행렬
m
−
1
{\displaystyle m-1}
0
하삼각 행렬
1
n
−
1
{\displaystyle n-1}
상헤센베르크 행렬
m
−
1
{\displaystyle m-1}
1
하헤센베르크 행렬
띠저장 [ 편집 ] 컴퓨팅 에서, 좁은 대역폭의 띠행렬을 더 작은 크기의 행렬로서 저장하여 행렬 알고리즘의 저장 효율을 높일 수 있다. 이를 띠저장 (-貯藏, 영어 : band storage )이라고 한다.
구체적으로, 하대역폭
p
{\displaystyle p}
q
{\displaystyle q}
n
×
n
{\displaystyle n\times n}
M
{\displaystyle M}
(
p
+
q
+
1
)
×
n
{\displaystyle (p+q+1)\times n}
band
(
M
)
{\displaystyle \operatorname {band} (M)}
p
,
q
≪
n
{\displaystyle p,q\ll n}
[1] :17, §1.2.5, (1.2.1)
band
(
M
)
i
j
=
{
M
i
+
j
−
q
−
1
,
j
i
+
j
−
q
−
1
∈
{
1
,
…
,
m
}
0
i
+
j
−
q
−
1
∉
{
1
,
…
,
m
}
{\displaystyle \operatorname {band} (M)_{ij}={\begin{cases}M_{i+j-q-1,j}&i+j-q-1\in \{1,\dots ,m\}\\0&i+j-q-1\not \in \{1,\dots ,m\}\end{cases}}}
예를 들어, 하대역폭 1 및 상대역폭 1를 갖는 6×6 띠행렬
M
=
(
M
11
M
12
0
0
0
0
M
21
M
22
M
23
0
0
0
0
M
32
M
33
M
34
0
0
0
0
M
43
M
44
M
45
0
0
0
0
M
54
M
55
M
56
0
0
0
0
M
65
M
66
)
{\displaystyle M={\begin{pmatrix}M_{11}&M_{12}&0&0&0&0\\M_{21}&M_{22}&M_{23}&0&0&0\\0&M_{32}&M_{33}&M_{34}&0&0\\0&0&M_{43}&M_{44}&M_{45}&0\\0&0&0&M_{54}&M_{55}&M_{56}\\0&0&0&0&M_{65}&M_{66}\\\end{pmatrix}}}
은 다음과 같은 3×6행렬로 저장할 수 있다.
band
(
M
)
=
(
0
M
12
M
23
M
34
M
45
M
56
M
11
M
22
M
33
M
44
M
55
M
66
M
21
M
32
M
43
M
54
M
65
0
)
{\displaystyle \operatorname {band} (M)={\begin{pmatrix}0&M_{12}&M_{23}&M_{34}&M_{45}&M_{56}\\M_{11}&M_{22}&M_{33}&M_{44}&M_{55}&M_{66}\\M_{21}&M_{32}&M_{43}&M_{54}&M_{65}&0\end{pmatrix}}}
같이 보기 [ 편집 ]
↑ 가 나 다 라 마 Golub, Gene H.; Van Loan, Charles F. (2013). 《Matrix Computations》. Johns Hopkins Studies in the Mathematical Sciences (영어) 4판. Baltimore: The Johns Hopkins University Press. ISBN 978-1-4214-0794-4 LCCN 2012943449 .
외부 링크 [ 편집 ]