프레넬 방정식

프레넬 방정식

프레넬 방정식(Fresnel equations) 또는 프레넬 공식(Fresnel's formulas)은 반사계수와 투과계수에 관한 것으로 한 매질과 광학적 특성 즉, 굴절률이 다른 매질의 계면에서 반사 또는 투과 진폭을 입사진폭으로 나눈 값을 말한다. 프랑스의 물리학자 오귀스탱 장 프레넬이 유도하였다.

개요

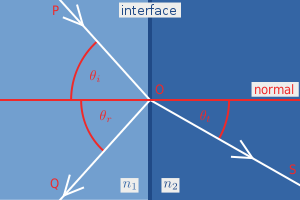
굴절률이 n₁인 매질에서 n₂인 매질로 빛이 투과할 때 반사와 굴절이 일어난다. 프레넬 방정식은 이 성질을 반사계수, 투과계수로 나누어 성분을 분석하여 표현한 방정식이다.

이 방정식에는 간단한 가정이 있는데, 첫 번째는 빛이 한 매질에서 다른 매질로 투과할 때, 그 면이 균일하고 평평한 평면이며, 둘째는 빛이 투과할 때 평면파라는 것이다.

진폭 방정식

진폭 방정식(amplitude equations)은 빛을 전자기파로 취급하여 반사의 법칙, 굴절의 법칙과 이들의 반사광과 굴절광의 세기를 표현한 것이다. 빛이 경계면을 지날 때의 전기장과 자기장의 경계조건을 빛의 파동 방정식에 적용하여 구현하였다.

프레넬 방정식에 쓰이는 변수들

표기법

입사파를 i, 반사파를 r, 투과파를 t로 쓰자.

반사, 굴절

입사파와 반사파, 굴절파의 위상은 같다.

${\boldsymbol {K}}_{i}{\boldsymbol {r}}-\omega t={\boldsymbol {K}}_{r}{\boldsymbol {r}}-\omega t={\boldsymbol {K}}_{t}{\boldsymbol {r}}-\omega t$

${\boldsymbol {K}}_{i}=K_{i}\sin \theta _{i}{\bar {x}}+K_{i}\cos \theta _{i}{\bar {z}}$

${\boldsymbol {K}}_{r}=K_{r}\sin \theta _{r}{\bar {x}}-K_{r}\cos \theta _{r}{\bar {z}}$

${\boldsymbol {K}}_{t}=K_{t}\sin \theta _{t}{\bar {x}}+K_{t}\cos \theta _{t}{\bar {z}}$

$z=0$ 일때

$K_{i}\sin \theta _{i}{\bar {x}}=K_{r}\sin \theta _{r}{\bar {x}}=K_{t}\sin \theta _{t}{\bar {x}}$

$K_{i}\sin \theta _{i}=K_{r}\sin \theta _{r}=K_{t}\sin \theta _{t}\$

이고

$K=n{\frac {\omega }{c}}$

$n_{i}=n_{r}$

이므로

$\sin \theta _{i}=\sin \theta _{r}$

$\theta _{i}=\theta _{r}$

을 만족한다 이를 반사의 법칙이라고 한다. 그리고

$n_{i}\sin \theta _{i}=n_{t}\sin \theta _{t}$

이다. 이를 스넬의 법칙이라고 한다.

파동방정식

전자기파인 빛을 파동형태로 나타낸 방정식으로 빛이 투과하는 경계면과 법선에 대하여 입사파, 투과파, 반사파로 나누어 나타낼 수 있으며, 각 파들의 계수들은 서로 관련이 있다.

멕스웰 방정식 및 표기법은 다음과 같다

${\boldsymbol {K}}\times {\boldsymbol {E}}={\omega }{\boldsymbol {B}}={\omega }{\mu }{\boldsymbol {H}}$

${\boldsymbol {H}}={\frac {n}{{\omega }{\mu }}}{\bar {k}}\times {\boldsymbol {E}}$

$\tau ={\boldsymbol {K}}{\boldsymbol {r}}-\omega t$

입사파

빛이 경계면에 입사하는 파로 전기장과 자기장의 각각의 x, y, z성분은 다음과 같다.

$E_{x}^{i}=-I_{\parallel }\cos \theta _{i}e^{i\tau _{i}}$

$E_{y}^{i}=I_{\bot }e^{i\tau _{i}}$

$E_{z}^{i}=I_{\parallel }\sin \theta _{i}e^{i\tau _{i}}$

$H_{x}^{i}=-I_{\bot }\cos \theta _{i}{\frac {n_{i}}{\mu _{i}c}}e^{i\tau _{i}}$

$H_{y}^{i}=-I_{\parallel }{\frac {n_{i}}{\mu _{i}c}}e^{i\tau _{i}}$

$H_{z}^{i}=I_{\bot }\sin \theta _{i}{\frac {n_{i}}{\mu _{i}c}}e^{i\tau _{i}}$

투과파

빛이 경계면을 투과하는 파로 전기장과 자기장의 각각의 x, y, z성분은 다음과 같다.

$E_{x}^{t}=-T_{\parallel }\cos \theta _{t}e^{i\tau _{t}}$

$E_{y}^{t}=T_{\bot }e^{i\tau _{t}}$

$E_{z}^{t}=T_{\parallel }\sin \theta _{t}e^{i\tau _{t}}$

$H_{x}^{t}=-T_{\bot }\cos \theta _{t}{\frac {n_{t}}{\mu _{t}c}}e^{i\tau _{t}}$

$H_{y}^{t}=-T_{\parallel }{\frac {n_{t}}{\mu _{t}c}}e^{i\tau _{t}}$

$H_{z}^{t}=T_{\bot }\sin \theta _{t}{\frac {n_{t}}{\mu _{t}c}}e^{i\tau _{t}}$

반사파

빛이 반사하는 파로 전기장과 자기장의 각각의 x, y, z성분은 다음과 같다.

$E_{x}^{r}=-R_{\parallel }\cos \theta _{r}e^{i\tau _{r}}$

$E_{y}^{r}=R_{\bot }e^{i\tau _{r}}$

$E_{z}^{r}=R_{\parallel }\sin \theta _{r}e^{i\tau _{r}}$

$H_{x}^{r}=-R_{\bot }\cos \theta _{r}{\frac {n_{t}}{\mu _{r}c}}e^{i\tau _{r}}$

$H_{y}^{r}=-R_{\parallel }{\frac {n_{r}}{\mu _{r}c}}e^{i\tau _{r}}$

$H_{z}^{r}=R_{\bot }\sin \theta _{r}{\frac {n_{r}}{\mu _{r}c}}e^{i\tau _{r}}$

경계조건

멕스웰 방정식 경계조건

${\bar {z}}\times \left({\boldsymbol {E_{2}}}-{\boldsymbol {E_{1}}}\right)=0$

${\bar {z}}\cdot \left({\boldsymbol {D_{2}}}-{\boldsymbol {D_{1}}}\right)=0$

${\bar {z}}\times \left({\boldsymbol {H_{2}}}-{\boldsymbol {H_{1}}}\right)=0$

${\bar {z}}\cdot \left({\boldsymbol {B_{2}}}-{\boldsymbol {B_{1}}}\right)=0$

이를 풀어 쓰면 다음과 같다

$E_{x}^{i}+E_{x}^{r}=E_{x}^{t}$

$E_{y}^{i}+E_{y}^{r}=E_{y}^{t}$

$H_{x}^{i}+H_{x}^{r}=H_{x}^{t}$

$H_{y}^{i}+H_{y}^{r}=H_{y}^{t}$

$D_{z}^{i}+D_{z}^{r}=D_{z}^{t}$

$B_{z}^{i}+B_{z}^{r}=B_{z}^{t}$

이때 경계면에서는 $z=0$ 이므로 다음과 같다.

$\tau _{i}=\tau _{r}=\tau _{t}$

프레넬 계수

주어진 프레넬 방정식에 경계조건을 대입하면 방정식의 계수를 구할 수 있다. 이들을 프레넬 계수(Fresnell coefficients)라고 하고, 다음과 같다.

$R_{\bot }={\frac {n_{1}\cos \theta _{\text{i}}-n_{2}\cos \theta _{\text{t}}}{n_{1}\cos \theta _{\text{i}}+n_{2}\cos \theta _{\text{t}}}}I_{\bot }$

$T_{\bot }={\frac {2n_{1}\cos \theta _{\text{i}}}{n_{1}\cos \theta _{\text{i}}+n_{2}\cos \theta _{\text{t}}}}I_{\bot }$

$R_{\parallel }={\frac {n_{2}\cos \theta _{\text{i}}-n_{1}\cos \theta _{\text{t}}}{n_{1}\cos \theta _{\text{t}}+n_{2}\cos \theta _{\text{i}}}}I_{\parallel }$

$T_{\parallel }={\frac {2n_{1}\cos \theta _{\text{i}}}{n_{1}\cos \theta _{\text{t}}+n_{2}\cos \theta _{\text{i}}}}I_{\parallel }$

반사율과 투과율

프레넬 계수를 통하여 반사율과, 투과율을 정의할 수 있는데, 프레넬 방정식은 전기장을 빛의 전자기를 서술하는 방정식이고, 반사율과 투과율은 빛의 세기를 나타내는 것이다. 그리고 반사율과, 투과율은 입사한 빛의 세기에 대해 얼마만큼 반사하거나 투과했는지의 비율을 나타낸 값이다. 따라서 이를 정리하면, 반사율($\mathbb {R}$)과 투과율($\mathbb {T}$)은 다음과 같다.

$\mathbb {R} ={\frac {{\left|R\right|}^{2}}{{\left|I\right|}^{2}}}$

$\mathbb {T} ={\frac {{\frac {\epsilon _{t}}{n_{t}}}{\left|T\right|}^{2}\cos \theta _{t}}{{\frac {\epsilon _{i}}{n_{i}}}{\left|I\right|}^{2}\cos \theta _{i}}}$

여기서 투과율은 입사한 빛과 투과한 빛의 매질과 유전율이 다르고 입사각과 투과각이 다르기 때문에 이를 고려한 값이다.

같이 보기

• 스넬의 법칙

외부 링크

• 프레넬 방정식 계산기