키르히호프의 전기회로 법칙
이 문서의 내용은 출처가 분명하지 않습니다. (2013년 10월) |
키르히호프의 법칙이란 구스타프 키르히호프(Gustav Kirchhoff)가 구한 전기 회로에 대한 법칙이다.
키르히호프의 전기회로 법칙은 1845년 구스타프 키르히호프가 처음으로 기술한 전기회로에서의 전하량과 에너지 보존을 다루는 2개의 이론식이다. 이 이론식은 전기공학분야에서 폭넓게 사용되고 또한 줄여서 키르히호프의 규칙(Kirchhoff's rules) 또는 키르히호프의 법칙이라 불린다(키르히호프 법칙 용어 참조).
키르히호프의 전류 법칙 (KCL,Kirchhoff's Current Law)[편집]

이 법칙은 키르히호프의 지점의 법칙, 키르히호프의 분기점 법칙(또는 노달법), 그리고 키르히호프의 첫 번째 법칙이다.
전류 법칙은 아래와 같다:
- 전류가 흐르는 즉 전기가 통과하는 분기점(선의 연결지점, 만나는 지점)에서, 전류의 합 즉 들어온 전류의 양과 나간 전류의 양의 합은 같다. 즉 0이다. 또는
- 도선망(회로)안에서 전류의 대수적 합은 0이다.(단, 들어온 전류의 양을 양수로, 나아간 전류의 양을 음수로 가정한다 또한 도선상의 전류의 손실은 없다고 가정한다).
전류는 노드로부터 들어 오거나 나아가는 정수(양의 정수, 음의 정수)이다. 식은 아래와 같다:
n 노드로부터 나아가거나 들어 가는 가지의 전체 숫자이다.
(위의 식을 풀어서 쓰면: )
(그림을 예를 들면: 이면 가 되고 이 된다.)
다시 이 식을 복소수화(일반화) 하면:
사용되는 곳:
키르히호프의 매트릭스 버전이 SPICE와 같은 모든 반도체 디자인 회로 시뮬레이션 소프트웨어의 기본 법칙으로 적용된다.
(지금 보이는 이 간단한 식이 이후에 모든 선형회로의 강력한 기초 법칙으로 모든 회로를 해석하고 반도체를 디자인하는 기본 법칙으로도 적용된다.)
키르히호프의 전압 법칙 (KVL,Kirchhoff's Voltage Law)[편집]
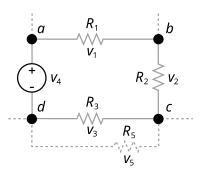
이 법칙을 키르히호프의 두 번째 법칙, 키르히호프의 루프의 법칙으로 부른다.
이 에너지 보존의 원칙은 아래와 같이 적용된다.(참고: 옴의 법칙 V=IR(V: 전압, I: 전류의 세기, R: 전기저항)은 키르히호프의 제2법칙의 가장 간단한 형태이다.)
- 닫힌 하나의 루프안 전압(전위차)의 합은 0이다.
- 또는
- 다르게 표현하면, 폐쇄된 회로의 인가된 전원의 합과 분배된 전위의 차의 합은 그 루프 안에서 등가한다.
- 또는
- 하나의 루프안에서 도체에 인가된(-걸린) 전압의 대수의 합과 그 루프에 인가한(공급된) 전체 전원 대수의 합은 같다.
KCL과 같이 식으로 표현하면, 아래와 같다:
여기서 n 은 측정된 전체 전압의 개수이다.
(예를 들면:)
다시 일반화(복소수화)하면:
이 법칙은 에너지의 인가와 출력, 공급과 소비의 포텐셜장(에너지보유장) 기초 원칙이 된다.(루프안에서의 에너지는 소멸되지 않는 다는 가정 하에서이다.) 인가된 전압 포텐셜, 완전히 폐쇄된 루프의 전하량 증가하거나 감소하지 않으며, 처음 인가된 전하량을 유지한다.
- 한계점
패러데이의 전자기 유도 법칙은 자기장이 변하는 곳에 있는 도체에 전위차(전압)가 발생한다고 하였다. 실제적으로 전자기장에서는 전하량 보존의 법칙이 성립되지 않는다. 실질적인 회로의 상태에서는 완전하고 완벽한 폐쇄 회로를 만들수 없으면, KVL에 존재하는 회로는 존재하지 않는다.









