정규 언어

위키백과, 우리 모두의 백과사전.

정규 언어(regular language), 합리적 언어(rational language)[1][2]는 이론 전산학, 형식 언어 이론에서 정규 표현식을 이용하여 표현할 수 있는 형식 언어이다.

정규 언어는 유한 상태 기계가 인지하는 언어로 정의할 수도 있다. 정규 표현식과 유한 상태 기계의 등가성은 클레이니의 정리로 알려져 있다.[3] 촘스키 위계에서 정규 언어는 3형 문법(정규 문법)에 의해 생성되는 언어로 정의된다.

정규 언어는 입력 구문 분석(파싱)과 프로그래밍 언어 설계에 매우 유용하다.

정의[편집]

<nowiki /> 정규 표현식 문서를 참고하십시오.

알파벳 Σ 위의 정규 언어의 집합은 다음과 같이 재귀적으로 정의할 수 있다.

  • 공집합 Ø은 정규 언어이다.
  • 각 글자 a ∈ Σ에 대해 한원소집합 {a}는 정규 언어이다.
  • A가 정규 언어이면, 클레이니 스타를 붙인 A*도 정규 언어이다. (따라서 빈 문자열로만 이루어진 {ε}도 정규 언어이다.)
  • A와 B가 정규 언어이면, 합집합 A ∪ B와 문자열 연결 AB도 정규 언어이다.
  • 그 밖의 언어는 정규 언어가 아니다.

예시[편집]

유한한 언어는 모두 정규 언어이다. 특히 {ε} = Ø*도 정규 언어이다. 알파벳 {a, b} 위의 정규 언어의 예로는 a를 짝수 개 포함하는 모든 문자열의 집합이나, a 여러 개 뒤에 b 여러 개가 오는 꼴인 모든 문자열의 집합 따위가 있다.

정규 언어가 아닌 언어의 예로 { anbn | n ≥ 0 }이 있다.[4] 직관적으로 설명하면, 유한 상태 기계의 기억력은 유한하기 때문에 a가 몇 번 나왔는지 정확히 기억할 수 없으므로, 유한 상태 기계는 이 언어를 인지할 수 없기 때문이다.

동등한 형식화[편집]

형식언어 L이 정규 언어라는 것은 다음과 동치이다.

  1. L은 정규 표현식으로 나타낼 수 있다. (위의 정의)
  2. L은 비결정적 유한 상태 기계가 인지하는 언어이다.[a][b]
  3. L은 결정적 유한 상태 기계가 인지하는 언어이다.[c][d]
  4. L은 정규 문법이 생성하는 언어이다.[e][f]
  5. L은 교대 유한 상태 기계(alternating finite automaton)가 인지하는 언어이다.
  6. L은 양쪽 유한 상태 기계(two-way finite automaton)가 인지하는 언어이다.
  7. L은 접두사 문법(prefix grammar)이 생성하는 언어이다.
  8. L은 읽기 전용 튜링 기계가 인지하는 언어이다.
  9. L은 일변수(monadic) 2차 논리에서 정의할 수 있는 언어이다. (뷔히-엘고트-트라크텐브로트 정리)[5]

닫힘 성질[편집]

정규 언어의 집합은 여러 연산에 대해 닫혀 있다. K와 L이 정규 언어라면, 다음도 정규 언어이다.

결정 가능성[편집]

결정적 유한 상태 기계 A와 B가 주어졌을 때, 두 기계가 같은 언어를 인지하는지 결정할 수 있다.[9] 따라서 위의 닫힘 성질을 이용하면 두 기계가 인지하는 정규 언어 LA와 LB에 대해 다음 문제를 결정할 수 있다.

  • 포함: LA ⊆ LB인가?[g]
  • 서로소: LA ∩ LB = Ø인가?
  • 공집합: LA = Ø인가?
  • 전체집합: LA = Σ*인가?
  • 소속: 주어진 a ∈ Σ*에 대해, a ∈ LA인가?

촘스키 위계에서의 위치[편집]

촘스키 위계에서 정규 언어의 위치

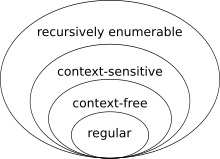
모든 정규 언어는 문맥 자유 언어이다. 그러나 반대는 성립하지 않는다. { anbn | n ≥ 0 }는 문맥 자유 언어이지만 정규 언어가 아닌 예이다.

주어진 언어가 정규 언어인지 알아보려면 흔히 마이힐-네로드 정리나 펌핑 보조정리를 사용한다. 그 밖에 정규 언어의 닫힘 성질이나 콜모고로프 복잡도를 사용하는 방법도 있다.[10]

내용주[편집]

  1. ↑ 1 ⇒ 2: 톰슨 구성
  2. ↑ 2 ⇒ 1: 클레이니 알고리즘 또는 아덴 보조정리
  3. ↑ 2 ⇒ 3: 멱집합 구성
  4. ↑ 3 ⇒ 2: 모든 결정적 유한 상태 기계는 비결정적 유한 상태 기계이므로.
  5. ↑ 2 ⇒ 4: Hopcroft, Ullman (1979), Theorem 9.2, p.219 참조
  6. ↑ 4 ⇒ 2: Hopcroft, Ullman (1979), Theorem 9.1, p.218 참조
  7. ↑ LA ∩ LB = LA인지 확인하면 된다.

참조주[편집]

  1. ↑ Ruslan Mitkov (2003). 《The Oxford Handbook of Computational Linguistics》. Oxford University Press. 754쪽. ISBN 978-0-19-927634-9. 
  2. ↑ Mark V. Lawson (2003). 《Finite Automata》. CRC Press. 98–103쪽. ISBN 978-1-58488-255-8. 
  3. ↑ Sheng Yu (1997). 〈Regular languages〉. Grzegorz Rozenberg and Arto Salomaa. 《Handbook of Formal Languages: Volume 1. Word, Language, Grammar》. Springer. 41쪽. ISBN 978-3-540-60420-4. 
  4. ↑ Eilenberg (1974), p. 16 (Example II, 2.8) and p. 25 (Example II, 5.2).
  5. ↑ M. Weyer: Chapter 12 - Decidability of S1S and S2S, p. 219, Theorem 12.26. In: Erich Grädel, Wolfgang Thomas, Thomas Wilke (Eds.): Automata, Logics, and Infinite Games: A Guide to Current Research. Lecture Notes in Computer Science 2500, Springer 2002.
  6. ↑ Salomaa (1981), 28쪽.
  7. ↑ Salomaa (1981), 27쪽.
  8. ↑ Hopcroft & Ullman (1979), 72쪽.
  9. ↑ Hopcroft, Ullman (1979), Theorem 3.8, p.64; Theorem 3.10, p.67도 참조.
  10. ↑ Hromkovič, Juraj (2004). 《Theoretical computer science: Introduction to Automata, Computability, Complexity, Algorithmics, Randomization, Communication, and Cryptography》. Springer. 76–77쪽. ISBN 3-540-14015-8. OCLC 53007120. 

참고 문헌[편집]

  • Berstel, Jean; Reutenauer, Christophe (2011). 《Noncommutative rational series with applications》. Encyclopedia of Mathematics and Its Applications 137. Cambridge: Cambridge University Press. ISBN 978-0-521-19022-0. Zbl 1250.68007. 
  • Eilenberg, Samuel (1974). 《Automata, Languages, and Machines. Volume A》. Pure and Applied Mathematics 58. New York: Academic Press. Zbl 0317.94045. 
  • Salomaa, Arto (1981). 《Jewels of Formal Language Theory》. Pitman Publishing. ISBN 0-273-08522-0. Zbl 0487.68064. 
  • Sipser, Michael (1997). 《Introduction to the Theory of Computation》. PWS Publishing. ISBN 0-534-94728-X. Zbl 1169.68300.  Chapter 1: Regular Languages, pp. 31–90. Subsection "Decidable Problems Concerning Regular Languages" of section 4.1: Decidable Languages, pp. 152–155.
  • Philippe Flajolet and Robert Sedgewick, Analytic Combinatorics: Symbolic Combinatorics. Online book, 2002.
  • John E. Hopcroft; Jeffrey D. Ullman (1979). 《Introduction to Automata Theory, Languages, and Computation》. Addison-Wesley. ISBN 0-201-02988-X. 
  • Alfred V. Aho and John E. Hopcroft and Jeffrey D. Ullman (1974). 《The Design and Analysis of Computer Algorithms》. Addison-Wesley. 

같이 보기[편집]

외부 링크[편집]

위키미디어 공용에 관련된
미디어 분류가 있습니다.
원본 주소 "https://ko.wikipedia.org/w/index.php?title=정규_언어&oldid=36775429"