애트우드 기계

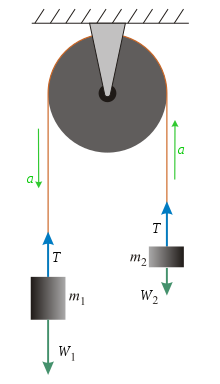
애트우드 기계(Atwood machine)는 1784년에 조지 애트우드가 등가속도 운동에서 뉴턴의 운동 법칙을 증명하기 위해 고안한 실험 장치이다. 고전역학의 기본적 원리를 설명하는 수업 자료로 종종 사용된다.

이상적인 애트우드 기계는 질량 $m_{1}$, $m_{2}$인 물체 두 개를 질량과 신축성을 무시할 수 있는 줄로 연결하여 질량을 무시할 수 있는 도르래에 걸어놓은 형태이다.

$m_{1}$＝$m_{2}$라면, 질량의 위치에 관계없이 기계는 역학적 평형을 이룬다.

$m_{1}$≠$m_{2}$라면, 두 질량은 일정한 가속도로 운동하게 된다.

등가속도 방정식

애트우드 기계를 간략하게 표현한 자유물체도. 가속도 벡터상에서 $m_{1}$이 아래로 운동하고 $m_{2}$가 위로 운동하므로, $m_{1}$＞$m_{2}$라는 사실을 알 수 있다.

힘을 분석하여 가속도의 방정식을 유도할 수 있다.

줄의 질량과 신축성, 도르래의 질량을 무시할 수 있다고 할 때, 이 계에서 고려해야 하는 힘은 장력($T$), 두 물체의 무게($W_{1}$과 $W_{2}$) 뿐이다. 가속도를 알아내기 위해 두 물체에 각각 작용하는 힘을 밝힐 필요가 있다.

뉴턴 제2법칙을 사용하여($m_{1}$＞$m_{2}$라고 기호 약속한다) 가속도($a$)를 구하기 위한 연립 방정식을 세울 수 있다.

가속도 $a$는 $m_{1}$에서는 아래 방향이 양의 방향, $m_{2}$에서는 위 방향이 양의 방향이라고 약속하자. $m_{1}$과 $m_{2}$의 무게는 각각 $W_{1}=m_{1}g$와 $W_{2}=m_{2}g$로 나타난다.

m₁에 작용하는 힘은

$\;m_{1}g-T=m_{1}a$

m₂에 작용하는 힘은

$\;T-m_{2}g=m_{2}a$

위의 두 방정식을 통째로 더하면 다음 식을 얻는다.

$\;m_{1}g-m_{2}g=m_{1}a+m_{2}a$,

그러므로 가속도 식을 다음과 같이 얻을 수 있다.

$a={m_{1}-m_{2} \over m_{1}+m_{2}}g$

역으로, 물체들의 운동 시간을 측정하여 등가속도 운동식 $d={1 \over 2}at^{2}$에 대입 계산함으로써 중력가속도 $g$를 구할 수도 있다.

라그랑주 역학에서 운동방정식을 유도할 때도 애트우드 기계가 사용되는 경우도 있다.

장력 방정식

장력을 알아볼 때는, 앞에서 구한 가속도를 두 물체의 힘 방정식 중 어느 한 쪽에 대입하면 된다.

$a={m_{1}-m_{2} \over m_{1}+m_{2}}g$

예컨대 이것을 $m_{1}a=m_{1}g-T$에 대입하면,

$T={2gm_{1}m_{2} \over m_{1}+m_{2}}$를 얻는다.

이와 같은 방법으로 장력을 얻을 수 있다.

관성과 마찰을 반영한 방정식

$m_{1}$과 $m_{2}$의 질량 차 이가 매우 작다면, 반경 $r$인 도르래의 회전관성 $I$를 무시할 수 없다. 줄이 미끄러지지 않는 상황에서 도르래의 각가속도 $\alpha$는 다음과 같이 주어진다.

$\alpha ={a \over r}$

이때 알짜 회전력 $\tau _{net}$는 다음과 같다.

$\tau _{net}=\left(T_{1}-T_{2}\right)r-\tau _{friction}=I\alpha$

매달린 물체들에 뉴턴 제2법칙을 적용한 것과 조합하면 다음과 같은 $a$, $T_{1}$, $T_{2}$를 얻는다.

가속도 $a$는

$a={{(m_{1}-m_{2})-{\tau _{friction} \over rg}} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}g$

줄의 $m_{1}$에 가장 가까운 부분의 장력 $T_{1}$은

$T_{1}={{m_{1}g(2m_{2}+{{I} \over {r^{2}}}+{{\tau _{friction}} \over {rg}})} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}$

줄의 $m_{2}$에 가장 가까운 부분의 장력 $T_{2}$는

$T_{2}={{m_{2}g(2m_{1}+{{I} \over {r^{2}}}+{{\tau _{friction}} \over {rg}})} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}$

줄의 마찰을 무시한다면(하지만 도르래의 관성과 도르래에 걸친 줄의 변형력은 무시할 수 없다), 다음과 같이 방정식을 간략화할 수 있다.

가속도 $a$는

$a={{(m_{1}-m_{2})} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}g$

줄의 $m_{1}$에 가장 가까운 부분의 장력 $T_{1}$은

$T_{1}={{m_{1}g(2m_{2}+{{I} \over {r^{2}}})} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}$

줄의 $m_{2}$에 가장 가까운 부분의 장력 $T_{2}$는

$T_{2}={{m_{2}g(2m_{1}+{{I} \over {r^{2}}})} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}$

같이 보기

• 캐터의 진자
• 흔들리는 애트우드 기계

외부 링크

• Professor Greenslade's account on the Atwood Machine Archived 2015년 1월 19일 - 웨이백 머신
• "Atwood's Machine" by Enrique Zeleny, The Wolfram Demonstrations Project.