선형 보간법

선형 보간법(線型補間法, linear interpolation)은 끝점의 값이 주어졌을 때 그 사이에 위치한 값을 추정하기 위하여 직선 거리에 따라 선형적으로 계산하는 방법이다.

두 빨간색 점 사이에 있는 파랑색 점의 위치를 추정하기 위하여 선형 보간법을 사용할 수 있다.

예시

예를 들어, 오른쪽 그림과 같이, 두 끝점 $(x_{0},y_{0})$와 $(x_{1},y_{1})$가 주어져 있을 때, 그 사이에 위치한 $(x,y)$의 값을 추정하기 위해 두 점 사이에 직선을 긋고 다음과 같은 비례식을 구성할 수 있다.

${\frac {y-y_{0}}{x-x_{0}}}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}$

이 수식을 풀면, 어떤 주어진 값 $x$에 대한 $y$ 값을 다음과 같이 구할 수 있다.

$y=y_{0}+(y_{1}-y_{0}){\frac {x-x_{0}}{x_{1}-x_{0}}}$

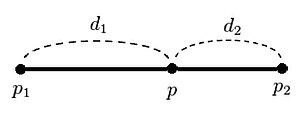
일반화

p1과 p2 사이에 있는 점 p의 값을 추정하기 위해 선형 보간법을 사용할 수 있다.

일반적으로 두 지점 $p_{1},p_{2}$에서의 데이터 값이 각각 $f(p_{1}),f(p_{2})$일 때, $p_{1},p_{2}$ 사이의 임의의 지점 $p$에서의 데이터 값 $f(p)$는 다음과 같이 계산할 수 있다.

$f(p)={\frac {d_{2}}{d_{1}+d_{2}}}f(p_{1})+{\frac {d_{1}}{d_{1}+d_{2}}}f(p_{2})$

단, $d_{1}$은 $p$에서 $p_{1}$까지의 거리, $d_{2}$는 $p$에서 $p_{2}$까지의 거리를 말한다.

만일 거리의 비를 합이 1이 되도록 정규화하면 ($d1+d2=1$) 위 식은 다음과 같이 단순화될 수 있다.

$f(p)={d_{2}}f(p_{1})+{d_{1}}f(p_{2})$

확장

선형 보간법은 1차원 직선상에서 이루어지는 보간법이다. 이를 2차원으로 확장하여 평면에 적용한 것이 이중 선형 보간법(bilinear interpolation)이고, 이를 3차원으로 확장하여 입방체에 적용한 것이 삼중 선형 보간법(trilinear interpolation)이다.

프로그래밍

선형 보간법은 다음과 같은 방법으로 프로그래밍을 할 수 있다.

// p1,p2를 d1:d2로 분할하는 p를 리턴한다. (단, d1+d2=1)
float lerp(float p1, float p2, float d1) {
  return (1-d1)*p1 + d1*p2;
}

p1, p2사이의 임의의 지점 p에서의 데이터값 f(p)는 다음과 같다.

$f(p)=d_{2}f(p_{1})+d_{1}f(p_{2})=f(d_{2}*p_{1})+f(d_{1}*p_{2})=f((1-d_{1})*p_{1}+d_{1}*p_{2})$

따라서, $f(p)=f(lerp(p1,p2,d1))$

같이 보기

• 보간법
• 보외법

외부 링크

• 선형 보간법(linear, bilinear, trilinear interpolation)