사용자:Kwj2772/부분게임 완전 균형
게임 이론에서, 부분게임 완전 균형 (또는 부분게임 완전 내쉬 균형)은 순차적 게임에 사용되는 내쉬 균형을 개선한 것이다. 원 게임의 모든 부분게임에서 내쉬 균형이 되는 전략은 부분게임 완전 균형이다. 모든 유한한 전개형 게임은 부분게임 완전 균형이 존재한다. [1]
부분게임 완전 균형을 구하는 일반적인 방법은 역진귀납법이다. 게임의 가장 마지막 행위자가 자기의 효용을 극대화하기 위해서 어떤 행위를 할 것인지를 먼저 고려하고, 바로 앞 행위자는 뒤의 행위자가 할 선택을 고려하여 자신의 효용을 극대화하는 전략을 선택하는 방법으로 균형을 구한다.이 과정을 맨 처음 행위자에 이를 때까지 계속한다. 남아있는 전략은 완전한 정보의 유한 기간 전개형 게임의 모든 부분게임 완전 균형의 집합이다.[1] 그러나, 역진귀납법은 불완전 정보 게임에는 적용될 수 없다.
예시[편집]
역진귀납법을 통해 부분게임 완전 균형을 찾는 방법은 아래 그림 1을 통해 살펴본다. 행위자 1의 전략은 {Up, Uq, Dp, Dq}에 의해 주어지며, 행위자 2의 전략은 {T, B, L, R}이다. 이 예시에서 부분게임은 4개이며, 진부분게임은 3개이다.
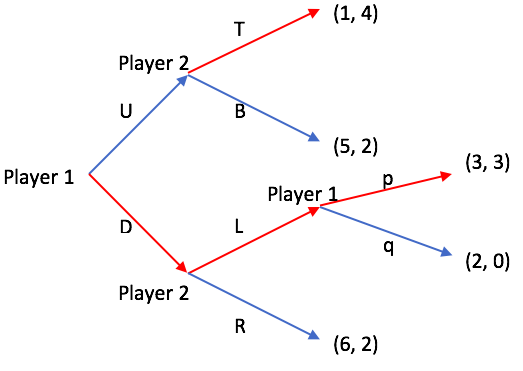
역진귀납법을 이용해 각 부분게임에서 경기자는 다음 전략을 취한다.
- 전략 p와 q에 대한 부분게임 : 행위자 1은 (3, 3)의 보수를 얻는 전략 p를 선택한다. 전략 L을 선택했을 때의 보수는 (3, 3)이다.
- 전략 L과 R에 대한 부분게임 : 행위자 2는 3> 2이므로 전략 L을 선택하고, 따라서 전략 D를 선택했을 때의 보수는 (3, 3)이다.
- 전략 T와 B에 대한 부분게임 : 행위자 2는 자기의 보수를 극대화하기 위해 전략 T를 선택한다. 따라서, 전략 U를 선택했을 때의 보수는 (1, 4)이다.
- 전략 U와 D에 대한 부분게임 : 행위자 1은 자기의 보수를 극대화하기 위해 전략 D를 선택한다.
따라서, 부분게임 완전 균형은 보수 (3, 3)을 얻는 {Dp, L}이다.
불완전 정보를 가진 전개형 게임은 그림 2에 제시되어 있다. 행위자 1의 전략 A, B를 나타내는 노드와 그 이후의 모든 전략을 나타낸 것이 하나의 부분게임이다. 행위자 2의 노드는 같은 정보집합의 일부이기 때문에 부분게임이 아니다.

첫번째 보수행렬은 전개형 게임의 전체를 정규형으로 나타낸 것이다. 주어진 정보에 따르면 (UA, X), (DA, Y), (DB, Y)가 모두 내쉬 균형이다.
두번째 보수행렬은 행위자 1의 두번째 노드부터 시작하는 부분게임을 정규형으로 나타낸 것이다. 여기에서 부분게임의 내쉬 균형은 (A, X)이다.
전체 게임의 내쉬 균형 (DA, Y)와 (DB, Y)는 부분게임 완전 균형이 아니다. 내쉬 균형 중 (UA, X)가 부분게임 완전 균형이다.[2]
이 게임을 풀기 위해서는 부분게임 1에서 상호간의 최적 반응을 구하여 내쉬 균형을 찾고, 역진귀납법을 통해 부분게임 2에서 (A, X) 전략을 대입한다.[2]
여기서 점선은 행위자 2는 행위자 1이 A와 B 중 어느 것을 택할지 모른다는 것을 의미한다.


따라서, 부분게임 완전 균형은 (UA, X)이다.
참고 문헌[편집]
- ↑ 가 나 Osborne, M. J. (2004). 《An Introduction to Game Theory》. Oxford University Press.
- ↑ 가 나 Joel., Watson. 《Strategy : an introduction to game theory》 Thi판. New York. ISBN 9780393918380. OCLC 842323069.
외부 링크[편집]
- 불완전한 정보의 전개형 게임의 예
- gametheory.net에서 전개형 게임에서 부분게임 완전 균형을 찾는 자바 애플릿
