첨도
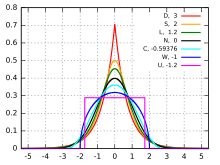
첨도(尖度, 영어: kurtosis 커토시스[*])는 확률분포의 꼬리가 두꺼운 정도를 나타내는 척도이다. 극단적인 편차 또는 이상치가 많을 수록 큰 값을 나타낸다. 첨도값(K)이 3에 가까우면 산포도가 정규분포에 가깝다. 3보다 작을 경우에는(K<3) 산포는 정규분포보다 꼬리가 얇은 분포로 생각할 수 있다, 첨도값이 3보다 큰 양수이면(K>3) 정규분포보다 꼬리가 두꺼운 분포로 판단할 수 있다.
정의[편집]
실확률변수 의 첨도 는 다음과 같다.
성질[편집]
n개의 확률변수 이 서로 독립이며, 또한 같은 분산을 갖는다고 하자. 그렇다면 다음이 성립한다.
만약 첨도가 정의될 수 있다면, 이는 적어도 1 이상이다. 첨도의 상한은 없으며, 임의로 클 수 있다.
참고 문헌[편집]
외부 링크[편집]
- “Excess coefficient”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- Weisstein, Eric Wolfgang. “Kurtosis”. 《Wolfram MathWorld》 (영어). Wolfram Research.


![{\displaystyle \operatorname {Kurt} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/785dd441133e5cafe6d6d5c700f5ed93fe96dfed)
![{\displaystyle \operatorname {Kurt} [X]={\frac {\operatorname {E} [(X-\operatorname {E} [X])^{4}]}{\operatorname {E} [(X-\operatorname {E} [X])^{2}]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc5edc576d8037e49bd5416f8d13af153b7cc4e7)

![{\displaystyle \operatorname {Kurt} [X_{1}+\cdots +X_{n}]={\frac {1}{n^{2}}}\left(\operatorname {Kurt} [X_{1}]+\cdots +\operatorname {Kurt} [X_{n}]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae6a1fdb26f8000b8931195dde580bc45c9a5c1e)
![{\displaystyle \operatorname {Kurt} [X]\geq 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9d83deed10369b9f74802593ce53e8b92c063e0)