이분법 (수학)

이분법을 폐구간 [a₁;b₁]에서 시작하여 여러번 반복하는 과정. 큰 빨간 점이 함수의 해이다.

수학에서 이분법(二分法, Bisection method)은 근이 반드시 존재하는 폐구간을 이분한 후, 이 중 근이 존재하는 하위 폐구간을 선택하는 것을 반복하여서 근을 찾는 알고리즘이다. 간단하고 견고하며 해의 대략적 위치를 안다면 일정 오차 내에 있는 1개의 해는 무조건 도출이 가능하나, 상대적으로 느린 방식이다. 이분법은 근이 존재한다는 것 자체를 전제로 구간을 설정하는 것이므로 근이 존재할 가능성은 100%이므로 방정식이 간단하고 근 자체가 가장 중요한 목적인 경우 가장 적합한 방법이다.

방법

기본적인 방법은 [a, b]에서 연속인 함수 f에 대하여 f(a)f(b) < 0,인 폐구간 [a,b]에 대해서 계속해서 ${\frac {\left|b+a\right|}{2}}$을 하여 나오는 또다른 수를 하나의 폐구간 끝점으로 잡은 새로운 폐구간을 만든다. 이와 같은 방법으로 계속 n번을 시행하게 되면 점점 함수 $f(x)=0\$를 만족하는 x에 다가가게 된다. 이런 방법을 이분법이라 한다.

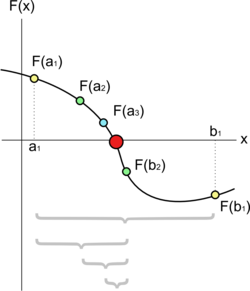
이분법은 f(a) 와 f(b) 가 다른 부호를 갖는 2개의 초기값 a 와 b를 필요로 한다. 중간값 정리에 의하여 연속함수 f는 폐구간 [a, b]에 대해서 최소한 한 개의 해를 가지게 되며, 이를 해 구간이라고 한다. 이제 중간 값 c = (a+b) / 2를 구한다. c가 해가 아닌 이상—가능성은 아주 희소하지만, 가능하다--, 2가지의 가능성이 있다. 첫째, f(a) 와 f(c) 가 다른 부호를 가지며 해 구간이다. 둘째, f(c) 와 f(b) 가 다른 부호를 가지며 해 구간이다. 2가지 가능성 중 해 구간을 선택(이분)한 후, 선택된 해 구간에 대해서 이분법 과정을 계속 반복한다. 이럴 경우 각 반복시마다 해 구간--f 가 0값을 가지는 값을 가지고 있는 구간—의 범위가 50%로 줄어든다. 목표로 하는 오차값 이하로 폐구간이 줄어들 때까지 이 과정을 반복한다. 찾고자 하는 값의 범위를 반복시마다 반으로 줄여서 찾는 전산 과학 분야의 이진 검색과 유사하다.

명시적으로 f(a) f(c) < 0 이면 c를 b의 새 값으로, f(b) f(c) < 0 이면 c를 a의 새 값으로 치환한다. 두 경우 다 새로운 f(a) 값과 f(b) 값은 서로 다른 부호를 가지게 되며, 그래서 이 새로운 작은 구간에서 다시 이분법을 적용할 수 있다. 허용 오차를 ε, n번째 구간을 $[a_{n},b_{n}]$이라고 할 때, 다음 조건이 만족될 때까지 반복한다.

$|a_{n}-b_{n}|<\epsilon$

또는 ${\frac {|a_{n}-b_{n}|}{|a_{n}|}}<\epsilon \quad or\quad |f(a_{n})|<\epsilon$

실제로 구현시에는 중간 값인 c 가 실제로 해인 경우를 고려해야 한다.

분석

f가 폐구간 [a, b]에서 연속 함수이며 f(a)f(b) < 0 이면, 이분법은 f의 해에 대해서 수렴한다. 사실상 오차가 각 반복마다 반으로 줄어드는 것이다. 그러므로 이 방법은 해에 대해서 선형적으로 수렴하나, 그 속도는 상당히 느리다. 다른 말로 표현하면 이분법은 f(a) 와 f(b) 가 서로 다른 부호를 가지고 있는 한 수렴하는 것을 보장한다.

이분법은 단일한 근의 추정위치를 가르쳐주기 보다는 오직 해가 존재하는 폐구간만을 결과로 제공한다. 따라서 다른 정보가 없을 때의 가장 좋은 근의 추정값은 찾아본 해 구간 중 가장 작은 해 구간의 중간 값이 된다. 이럴 경우, 이분법을 n번 반복하였을 때 오차의 절댓값은 아래의 값과 같다.

${\frac {\left|b-a\right|}{2^{n+1}}}.$

만일 해 구간의 양 끝 점이 하나라도 사용되었으며, 오차의 최댓값의 절댓값은 해 구간의 전체 길이인 아래와 같다.

${\frac {\left|b-a\right|}{2^{n}}},$

이 식은 이분법을 허용 가능한 오차의 범위까지 구하기 위해서 몇 번을 반복하여야 하는가를 미리 고려할 때 유용하다. 두 번째 식을 이용하여, 허용 가능한 오차 ε 이하의 추정 해를 구하고 싶다면 이분법을 아래의 식을 만족하는 n 번 이상 반복하여야 한다.

$n>\log _{2}{\frac {b-a}{\epsilon }}$

폐구간 [a,b] 내에서 f가 여러 개의 해를 가지고 있다면, 이분법은 그 중 하나의 해를 구할 것이다.

같이 보기

• 루트
• 할선법
• 뉴턴 방법

참고 문헌

• Abdelwahab Kharab; Ronald B. Guenther (2013). 《An Introduction to Numerical Methods A MATLAB Approach》 [이공학도를 위한 수치해석]. 학산미디어. ISBN 978-89-966211-8-8.