원환면 오류 정정 부호

원환면 오류 정정 부호(영어: Toric code)는 위상수학적 양자 오류 정정 부호이며, 2차원 스핀 격자에 정의된 안정자 부호의 예이다. 이는 양자 이중 모델 중 가장 간단하고 가장 잘 연구된 모델이다. 이는 또한 위상수학적 질서의 가장 간단한 예인 Z₂ 위상수학적 질서(1991년 Z ₂ 스핀 액체의 맥락에서 처음 연구됨)이기도 하다. 원환면 오류 정정 부호는 특정 극한에서 Z ₂ 격자 게이지 이론으로 볼 수도 있다. 알렉세이 키타예프가 소개했다.

원환면 오류 정정 부호는 원환면 모양을 갖는 주기적인 경계 조건 때문에 그러한 이름이 붙었다. 이러한 조건은 분석 연구에 유용한 모델 변환 불변성을 제공한다. 그러나 일부 실험에는 열린 경계 조건이 필요하므로 시스템을 2차원 곡면에 내장할 수 있다. 결과 부호는 일반적으로 평면 부호로 알려져 있다. 이는 전부는 아니지만 대부분의 경우 원환면 오류 정정 부호와 동일하게 행동한다.

오류 정정 및 계산

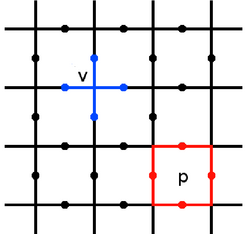
원환면 오류 정정 부호는 일반적으로 각 모서리에 스핀-½ 자유도가 있는 정사각형 격자로 선택되는 2차원 격자에 정의된다. 이들은 주기적으로 선택된다. 안정자 연산자는 각 꼭지점 $v$ 주위의 회전에 정의된다. 그리고 격자의 플라크 $p$는 (또는 면, 즉 이중 격자의 꼭지점) 다음과 같이

$A_{v}=\prod _{i\in v}\sigma _{i}^{x},\,\,B_{p}=\prod _{i\in p}\sigma _{i}^{z}$

정의된다. 여기서 $i\in v$는 꼭지점 $v$에 닿는 모서리를 나타낸다. 그리고 $i\in p$눈 플라크 $p$주변의 모서리를 나타낸다. 부호의 안정자 공간은 모든 안정자가 자명하게 작용하는 공간이므로 이 공간의 모든 상태 $|\psi \rangle$에 대해

$A_{v}|\phi \rangle =-|\phi \rangle$

원환면 오류 정정 부호의 경우 이 공간은 4차원이므로 2 큐비트의 양자 정보를 저장하는 데 사용할 수 있다. 이는 독립적인 안정자 연산자의 수를 고려함으로써 입증될 수 있다. 오류가 발생하면 상태가 안정자 공간 밖으로 이동하여 위의 조건이 유지되지 않는 꼭지점과 플라크가 생성된다. 이러한 위반 위치는 오류 수정에 사용될 수 있는 부호 징후이다.

원환면 오류 정정 부호의 한 부분이다. 꼭지점과 플라크가 강조 표시되어 있으며 안정 장치 정의에 사용되는 스핀도 함께 표시된다.

원환면 오류 정정 부호와 같은 위상수학적 부호의 고유한 특성은 안정자 위반이 준입자로 해석될 수 있다는 것이다. 특히 부호가

$A_{v}|\phi \rangle =-|\phi \rangle$

가 성립하는 상태 $|\phi \rangle$인 경우, 애니온으로 알려진 준입자 $e$는 꼭지점 $v$에 존재한다고 할 수 있다. 마찬가지로 $B_{p}$의 위반은 소위 플라크에 있는 $m$ 애니온들와 연관되어 있다. 따라서 안정자 공간은 애니온 진공에 해당한다. 단일 스핀 오류로 인해 애니온 쌍이 생성되어 격자 주위로 이동된다.

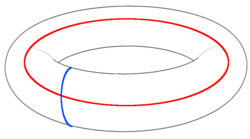
오류가 애니온 쌍을 생성하고 애니온을 이동하면 작동되는 모든 링크로 구성된 두 개를 연결하는 경로를 상상할 수 있다. 애니온들이 만나서 소멸되면 이 경로는 고리가 된다. 고리가 위상수학적으로 자명한 경우 저장된 정보에는 영향을 미치지 않는다. 이 경우 애니온들이 소멸하면 생성 및 전송과 관련된 모든 오류가 정정된다. 그러나 고리가 위상수학적으로 자명하지 않은 경우 애니온의 재소멸은 상태를 안정자 공간으로 반환하지만 저장된 정보에 대한 논리적 연산도 구현한다. 따라서 이 경우 오류는 정정되지 않고 통합된다.

원환면 위의 위상수학적으로 자명하지 않은 고리. 이 고리를 따라 이동하는 애니온들은 저장된 큐비트에서 파울리 연산자를 구현한다.

비트 오류와 페이즈 오류가 각각의 스핀에서 독립적으로 발생하는 잡음 모델을 생각하자. 오류가 발생할 확률은 둘 다 $p$라 하자. $p$가 낮으면 생성점에서 멀리 이동하지 않은 희박하게 분산된 쌍이 생성된다. 수정은 애니온이 생성된 쌍(동치류에 대해)을 식별한 다음 이를 다시 소멸시켜 오류를 제거함으로써 달성할 수 있다. 그러나 $p$가 증가함에 따라 위상수학적으로 자명하지 않은 고리가 형성될 위험 없이 애니온이 어떻게 쌍을 이룰 수 있는지에 대해 더욱 모호해진다. 이는 오류 정정이 거의 확실하게 성공할 임계 확률을 제공한다. 무작위 결합 이징 모델에 대한 사상을 통해 이 임계 확률은 약 11%인 것으로 나타났다.

다른 오류 모델도 고려하여 임계값을 찾을 수 있다. 지금까지 연구한 모든 사례에서 부호는 해싱 경계를 포화시키는 것으로 나타났다. 비트 오류가 페이즈 오류보다 더 자주 발생하거나 그 반대인 편향 오류와 같은 일부 오류 모델의 경우 최적의 임계값을 달성하기 위해 정사각형 격자 이외의 격자를 사용해야 한다.

이러한 임계값은 상한이며 이를 달성하기 위한 효율적인 알고리듬이 발견되지 않는 한 쓸모가 없다. 가장 잘 사용되는 알고리듬은 최소 가중치 완벽 매칭이다. 독립적인 비트 및 뒤집기 오류가 있는 잡음 모델에 적용하면 약 10.5%의 임계값이 달성된다. 이는 최대 11%에 약간 못 미치는 수준이다. 그러나 탈분극 잡음과 같이 비트 오류와 페이즈 오류 사이에 상관 관계가 있는 경우 매칭이 제대로 작동하지 않는다.

내결함성을 제공하는 부호의 성질과 함께 원환면 오류 정정 부호 내에 저장된 논리 정보에 대해 양자 계산을 수행하는 수단이 고려되었다. 안정 장치가 적용되지 않는 '구멍', 정점 또는 플라크를 사용하여 안정자 공간을 확장하면 많은 큐비트를 정정 부호에 인코딩할 수 있는 것으로 나타났다. 그러나 범용 게이트 세트는 유니터리 연산으로 내결함성을 구현할 수 없으므로 양자 컴퓨팅을 달성하려면 추가 기술이 필요하다. 예를 들어, 큐비트로 대체될 때 필요한 추가 게이트에서 순간 이동하는 데 사용되는 tidBits라는 인코딩된 양자 스텁을 통해 마법 상태를 준비함으로써 범용 양자 컴퓨팅을 달성할 수 있다. 더욱이, 마법 상태의 준비는 내결함성이 있어야 하며, 이는 잡음이 있는 마법 상태에 대한 마법 상태 증류를 통해 달성할 수 있다. 이 원리에 기초한 양자 계산을 위한 측정 기반 방식이 발견되었으며, 그 오류 임계값은 2차원 아키텍처에 대해 알려진 가장 높은 것이다.

해밀토니안과 자기 정정

원환면 오류 정정 부호의 안정화 연산자는 준국소적이므로 2차원 격자에서 서로 가까이 위치한 스핀에만 작용하므로 다음과 같은 해밀토니안을 정의하는 것이 비현실적이진 않다.

$H_{\rm {TC}}=-J\sum _{v}A_{v}-J\sum _{p}B_{p},\,\,\,J>0.$

이 해밀토니언의 바닥 상태 공간은 부호의 안정자 공간이다. 들뜬 상태는 애니온들의 상태와 동일하며, 에너지는 그 수에 비례한다. 따라서 국소적 오류는 차이에 의해 에너지적으로 억제되며, 이는 국소적 섭동에 대해 안정적인 것으로 나타났다. 그러나 그러한 섭동의 동적 효과는 여전히 정정부호에 문제를 일으킬 수 있다.

또한 이 간격은 부호에 열 오류에 대한 특정 탄력성을 제공하여 특정 중요한 시간 동안 거의 확실하게 수정이 가능하도록 한다. 이 시간은 $J$와 같이 증가한다. 그러나 이 결합의 임의적인 증가는 비현실적이므로 해밀토니안이 제공하는 보호에는 여전히 한계가 있다.

원환면 오류 정정 부호, 즉 평면 부호를 완전히 자가 교정되는 양자 메모리로 만드는 방법이 종종 고려된다. 자가 교정은 해밀토니안이 자연적으로 오류를 무기한으로 억제하여 열역학적 한계에서 벗어나는 수명으로 이어진다는 것을 의미한다. 이는 누군가 사이에 장거리 상호 작용이 있는 경우에만 원환면 오류 정정 부호에서 가능하다는 것이 밝혀졌다. 실험실에서 이를 실현하기 위한 제안이 있었다 또 다른 접근 방식은 모델을 더 높은 차원으로 일반화하는 것이다. 즉, 준국소적 상호 작용만 사용하여 4차원에서 자체 정정이 가능하다.

애니온 모델

위에서도 말했듯이 $e$ 그리고 $m$이라 불리는 준입자는 각각 모델의 꼭지점 및 플라크와 연관된다. 이러한 준입자는 꼬임의 자명하지 않은 효과로 인해 애니온들로 설명될 수 있다. 구체적으로 말하면, 두 종 모두 그 자체로는 보존적이지만, 두개의 $e$ 또는 $m$을 땋는 것은 아무런 효과가 없다. $e$와 $m$의 완전한 모노드로미는 $-1$의 페이즈를 생성할 것이다. 이러한 결과는 보손 또는 페르미온 통계와 일치하지 않으므로 애니온이다.

준입자의 애니온 상호 통계는 위상수학적으로 자명하지 않은 고리에 의해 수행되는 논리적 작업을 보여준다. 한 쌍 $e$ 애니온들의 생성을 고려하자. 이 쌍이 다시 소멸되기 전에 위 그림의 파란색 원환체에 표시된 것과 같이 위상학적으로 자명하지 않은 고리 주위에 하나가 전송된다. 상태는 안정자 공간으로 반환되지만 고리는 저장된 큐비트 중 하나에 대한 논리 연산을 구현한다. 만약에 $m$ 애니온들도 마찬가지로 논리 연산 위의 빨간색 고리를 통해 이동하면 결과도 발생한다. $-1$의 페이즈는 애니온들을 땋을 때 결과는 이러한 작용이 교환이 아니라 오히려 반교환임을 보여준다. 그러므로 이들은 저장된 큐비트 중 하나에 대한 $Z$와 $X$ 파울리 연산자로 해석될 수 있다. 이에 대응하는 다른 큐비트에 대한 파울리 연산자들은 파란색 고리를 따라가는 $m$ 애니온과 빨간색을 따라가는 $e$ 애니온에 해당한다. $e$과 $m$이 평행 경로를 통과하면 꼬임 현상이 발생하지 않는다. $-1$의 페이즈는 따라서 발생하지 않으며 해당 논리 연산이 교환한다. 이들은 서로 다른 큐비트에 작용하는 연산을 형성하므로 이는 예상한 대로이다.

$e$와 $m$ 애니온 둘 쌍으로 생성될 수 있다는 사실로 인해 이 두 준입자가 모두 자신의 반입자라는 것이 분명하다. $e$ 애니온 2개로 구성된 합성입자는 그러므로 애니온들은 진공과 동일하다. 왜냐하면 진공은 그러한 쌍을 생성할 수 있고 그러한 쌍은 진공으로 소멸될 것이기 때문이다. 따라서 이러한 합성입자는 땋임이 항상 완전히 자명하기 때문에 보존 통계를 갖는다. 비슷하게, $m$ 애니온 두 개의 합성입자는 진공과 동일하다. 그러한 합성입자의 생성은 애니온의 융합으로 알려져 있으며, 그 결과는 융합 규칙의 관점에서 기술될 수 있다. 이 경우에는 다음과 같은 형식을 취한다.

$e\times e=1,\,\,\,m\times m=1.$

여기서 $1$은 진공을 나타낸다. $e$ 하나와 $m$ 하나의 합성입자는 자명한 것이 아니다. 따라서 이는 모델의 또 다른 준입자를 구성하며 때로는 $\psi$과 같이 표시된다. 융합 규칙을 사용하여,

$e\times m=\psi .$

애니온의 땋임 통계를 통해, 두 $\psi$들의 단일 교환은 구성 요소 $e$과 $m$의 완전한 모노드로미를 포함하기 때문에, $-1$의 페이즈가 결과로 나올 것이다. 이는 $\psi$에 대한 페르미온 자체 통계를 의미한다.

일반화

오류 수정 부호를 형성하기 위해 원환면을 사용할 필요는 없다. 안정자 공간의 축퇴를 결정하는 위상수학적 특성을 갖는 다른 곡면도 사용될 수 있다. 일반적으로 위의 원리에 따라 2차원 스핀 격자에 정의된 양자 오류 정정 부호를 곡면 부호라고 한다.

고차원 스핀을 사용하여 유사한 부호를 정의하는 것도 가능하다. 이는 양자 이중 모델과 스트링-네트 모델 로, 누구든지 행동을 더 풍부하게 할 수 있으므로 보다 발전된 양자 계산 및 오류 수정 제안에 사용될 수 있다. 여기에는 아벨 애니온들이 포함된 모델뿐만 아니라 비아벨 통계가 포함된 모델도 포함된다.

실험 진전

원환면 오류 정정 부호의 성질을 가장 명확하게 보여주는 것은 상태 기반 접근 방식이다. 해밀토니안을 구현하려고 시도하기보다는 단순히 안정자 공간에 부호를 준비한다. 이 기술을 사용하여 실험을 통해 애니온의 생성, 전송 및 통계와 위상적 얽힘 엔트로피 측정을 입증할 수 있었다. 최근의 실험에서도 부호의 오류 정정 성질을 입증할 수 있었다.

원환면 오류 정정 부호의 실현과 해밀토니안을 사용한 일반화를 위해 조셉슨 접합을 사용하여 많은 진전이 이루어졌다. 해밀토니안이 어떻게 구현될 수 있는지에 대한 이론은 광범위한 위상수학적 정정 부호들에 대해 개발되었다. 작은 격자에 대한 원환면 오류 정정 부호 해밀토니안을 구현하고 축퇴된 바닥 상태에 의해 제공되는 양자 메모리를 입증하는 실험도 수행되었다.

실현을 위한 다른 이론적이고 실험적인 작업은 차가운 원자를 기반으로 한다. 위상수학적 질서의 최소 인스턴스에 관한 실험과 광학 격자를 사용하여 위상 부호를 구현하는 데 사용할 수 있는 방법 툴킷이 탐색되었다. 원환면 오류 정정 부호의 이러한 최소 인스턴스는 격리된 사각형 플라크 내에서 실험적으로 구현되었다. 해밀토니안과 소산 소음의 효과를 입증할 수 있는 리드버그 원자를 사용한 원환면 모델의 시뮬레이션도 진행되고 있다. 리드버그 원자 배열 실험에서는 얽힌 원자 배열을 일관되게 전달하여 2차원의 주기적인 경계 조건을 갖는 원환면 오류 정정 부호를 성공적으로 실현했다.