이진 검색 알고리즘
보이기
(이진 탐색에서 넘어옴)
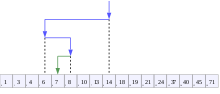
이진 검색 알고리즘(binary search algorithm)은 오름차순으로 정렬된 리스트에서 특정한 값의 위치를 찾는 알고리즘이다. 처음 중간의 값을 임의의 값으로 선택하여, 그 값과 찾고자 하는 값의 크고 작음을 비교하는 방식을 채택하고 있다. 처음 선택한 중앙값이 만약 찾는 값보다 크면 그 값은 새로운 최댓값이 되며, 작으면 그 값은 새로운 최솟값이 된다. 검색 원리상 정렬된 리스트에만 사용할 수 있다는 단점이 있지만, 검색이 반복될 때마다 목표값을 찾을 확률은 두 배가 되므로 속도가 빠르다는 장점이 있다.
의사 코드
[편집]BinarySearch(A[0..N-1], value, low, high) {
if (high < low)
return -1 // not found
mid = (low + high) / 2
if (A[mid] > value)
return BinarySearch(A, value, low, mid-1)
else if (A[mid] < value)
return BinarySearch(A, value, mid+1, high)
else
return mid // found
}
high와 low를 지정
[편집]binarySearch(A[0..N-1], value) {//k
low = 0
high = N - 1
while (low <= high) {
mid = (low + high) / 2
if (A[mid] > value)
high = mid - 1
else if (A[mid] < value)
low = mid + 1
else
return mid // found k
}
return -1 // not found k
}
소스 코드
[편집]// loop version : A[0 ~ N-1]
int binarySearch(int A[], int low, int high, int target){
while(low <= high){
int mid = (low + high) / 2;
if(A[mid] == target) return mid;
if(A[mid] > target) high = mid - 1;
else low = mid + 1;
}
return -1;
}
// recursive version : A[0 ~ N-1]
int binarySearchRecur(int A[], int low, int high, int target){
if(low > high) return -1;
int mid = (low + high) / 2;
if(A[mid] == target) return mid;
if(A[mid] > target){
return binarySearchRecur(A, low, mid-1, target);
}
return binarySearchRecur(A, mid+1, high, target);
}
// one-side(meta) binary search version : A[0 ~ N-1]
int metaBinarySearch(int A[], int low, int high, int target){
int bin = 1, idx = 0;
while(bin <= high) bin <<= 1;
for(bin >>= 1;; bin >>= 1){
int i = idx + bin;
if( i <= high && A[i] <= target){
if(A[i] == target) return i;
idx = i;
}
if(bin == 0) break;
}
return -1;
}
파이썬
[편집]def binarySearch(array, value, low, high):
if low > high:
return False
mid = (low+high) / 2
if array[mid] > value:
return binarySearch(array, value, low, mid-1)
elif array[mid] < value:
return binarySearch(array, value, mid+1, high)
else:
return mid
public int binarySearch(int[] arr, int target) {
int start = 0;
int end = arr.length - 1;
int mid = 0;
while (start <= end) {
mid = (start + end) / 2;
if (target == arr[mid]) {
return mid;
}else if (arr[mid] < target) {
start = mid + 1;
}else if (target < arr[mid]) {
end = mid - 1;
}
}
throw new NoSuchElementException("can't find target.");
}
| 이 글은 컴퓨터 과학에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. |
