회절

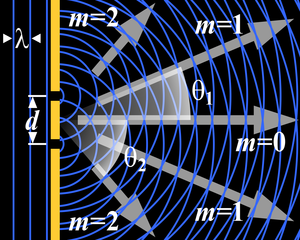
회절(回折, 영어: diffraction)은 대표적인 파동 현상 중의 하나이다. 고유어로 에돌이라고 하며 음파나 전파 또는 광파 등이 장애물이나 좁은 틈을 통과할 때, 파동이 그 뒤편(그림자 부분)까지 전파하는 현상이다.
간섭현상으로서의 회절 현상으로는 가시광이 회절격자에 의해 반사되는 경우, 엑스선이 고체 결정에 의해 반사되는 경우, 파장이 좁은 틈을 지날때 생기는 1~2차 회절 현상 등이 있다.
회절은 보통 장애물에 부딪혀서 발생하는 다양한 현상으로 언급된다. 예를 들어 굴절하는 빛 파동 또는, 음파 임피던스 ,음향 파동 등 이러한 것들은 회절 현상과 관련 되어 있다. 회절은 모든 파동에서 발생한다. 음파, 물결파, 자기파, 빛, 엑스선, 그리고 라디오파 같은 곳에서 볼 수 있다.
입자의 진행경로에 틈이 있는 장애물이 있으면 입자는 그 틈을 지나 직선으로 진행한다. 이와 달리 파동의 경우, 틈을 지나는 직선 경로뿐 아니라 그 주변의 일정 범위까지 돌아 들어간다. 이처럼 파동이 입자로서는 도저히 갈 수 없는 영역에 휘어져 도달하는 현상이 회절이다. 물결파를 좁은 틈으로 통과시켜 보면 회절을 쉽게 관찰할 수 있다.
회절의 정도는 틈의 크기와 파장에 영향을 받는다. 틈의 크기에 비해 파장이 길수록 회절이 더 많이 일어난다. 즉, 파장이 일정할 때 틈의 크기가 작을수록 회절이 잘 일어나, 직선의 파면을 가졌던 물결이 좁은 틈을 지나면 반원에 가까운 모양으로 퍼진다. 빛의 예로는 브래그의 법칙에 따라 nλ=2dsinθ으로 나타난다.
단일슬릿에 의한 빛의 회절[편집]
평면파로 슬릿에 도달한 파면 위의 모든 점은 호이겐스(Christiaan Huygens, 하위헌스라고도 부른다)의 원리에 따라 새로운 구면파의 파원이 된다. 이 파원을 앞으로 점파원이라 하자. 슬릿 상의 모든 점파원에서 생긴 구면파의 점 P에서의 중첩을 계산하면 점 P에서의 빛의 세기를 구할 수 있다.
슬릿 폭의 단위 길이당 전기장의 진폭을 라 하고, 슬릿을 m개의 구간으로 나누었을 때 그 중 하나의 작은 부분을 라 하면, 에 의한 P점에서의 전기장의 진폭()은
이다. 이 값을 슬릿의 전체 폭 b에 대하여 합하면 점 P에서의 진폭(E)은
이다.
위 식의 진폭과 위상을 평면파로 전파한다는 프라운호퍼 조건에 따라 근사한 후에 계산한다. 먼저 점 P에서의 진폭()을 근사해 보자. 슬릿상의 각 점파원에 의한 점 P에서의 진폭은 로 각각 다르지만 이므로 모든 에 대하여 로 근사하여 슬릿의 모든 점파원에 의한 점 P에서의 진폭을 으로 근사한다.
이번에는 점 P에서의 위상인 을 근사해 보자. 진폭에 비해서 위상은 각 점파원의 위치에 따라 심하게 변하므로 주의해야 한다. 슬릿에서 점 P로 진행하는 파동은 스크린이 멀리 있으므로 평면파라고 생각하면 [그림 2]와 같이 모든 점파원에서 점 P로 향하는 파동의 진행 방향은 평행하므로 로 근사할 수 있다.위의 두 근사를 대입하고 정리하면 점 P에서의 전기장(E)은
이 된다. 이 식을 적분
이다. 이때 새로운 변수 β는
이다.
눈으로 직접 관찰 가능한 값인 빛의 세기(I)는 전기장을 제곱한 값이다. 그런데 전기장(E)은 시간에 따라 매우 빠르게 변하는 값이므로 빛의 세기(I)는 아래와 같이 전기장을 제곱하여 평균한 값으로 구한다.
(슬릿의 중심 방향) 에서는이 되어 분자와 분모가 0이 되지만 β가 0에 가까워질수록 sinβ는 β와 같은 값을 가지게 되며 결국 β=0 일 때 극한의 성질에 의하여 이 된다. 그러므로 θ=0 일 때의 빛의 세기()는이다. 따라서 빛의 세기(I)는
으로 나타낼 수 있다. 식(7)을 간단히 해석해 보면 분모의은 점점 커지는데 비해서 분자의 은 0과 1 사이에서 진동하므로 β가 커짐에 따라 빛의 세기가 점점 약해 지면서 주기적으로 극대인 곳과 0인 곳이 나타남을 알 수 있다.
일상생활과 회절현상[편집]
담장 너머의 사람이 보이지는 않아도 말하는 소리는 들을 수 있다. 소리(음파)는 공기를 매질로 하는 파동이므로 회절이 일어난다. 따라서 담장 너머의 말소리는 담장 위쪽을 돌아 반대편까지 전달된다.
사진기의 조리개를 조이면 선명한 사진을 얻을 수 있지만 과도하게 조이면 오히려 사진의 품질이 떨어지기도 한다. 이것은 조리개를 구성하는 여러 개의 날 사이의 틈을 지나는 빛이 회절에 의해 분산되기 때문이다.
라디오의 AM방송은 FM방송에 비해서 수신이 잘 된다. 이는 AM방송에 쓰는 전파의 파장이 FM방송에 사용되는 파장의 길이보다 길어서 건물이나 장애물을 만났을 때 회절되어 구석구석 잘 전달되기 때문이다.
























