역제곱 법칙
역제곱 법칙(逆-法則, 영어: inverse square law)은 물리학의 여러 힘의 법칙에서, 어떤 힘의 크기가 거리의 제곱에 반비례하는 것을 가리키는 말이다. 이 규칙에 해당하는 것은 중력, 쿨롱의 법칙, 빛의 세기 등이 있다.
뉴턴의 중력 법칙[편집]
뉴턴의 중력 법칙은 다음과 같은 방정식으로 기술된다.
즉, 중력은 질량을 띤 두 물체의 거리의 제곱에 반비례한다.
- 는 중력상수
태양이나 행성 같은 우주의 모든 물체 사이에는 서로 당기는 힘 F가 작용하며, 물체의 종류 또는 물체 사이에 존재하는 매질(媒質)과는 관계없이 그 물체의 질량 m, m'의 곱에 비례하고, 두 물체의 질점 사이의 거리 r의 제곱에 반비례한다는 법칙을 말한다.
뉴턴은 태양과 행성 사이에서 작용하는 인력이 두 천체의 질량과 거리에 의해 결정되므로 어떤 특정한 천체에 국한되는 것이 아니라 질량이 있는 모든 물체 사이에 작용한다고 생각했다(만유 인력의 법칙).
쿨롱의 법칙[편집]
전자기력은 전하를 띤 두 물체의 거리의 제곱에 반비례한다. 여기서 k는 쿨롱 상수로,약 이다.
3차원[편집]
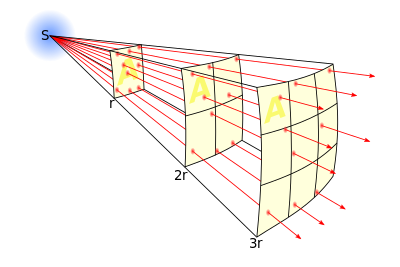
역제곱 법칙은 3차원 공간에서의 힘이 퍼지는 것으로 해석할 수 있다. 중력장과 전기장 등은 3차원 공간으로 퍼져 나가고, 이때 어떤 거리에 대해 퍼져 나가는 단면은 2차원이다. 즉, 힘은 넓이에 반비례하므로 거리의 제곱에 반비례해야 한다.
| 이 글은 물리학에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. |




