레드-블랙 트리

위키백과, 우리 모두의 백과사전.
Rubydragons (토론 | 기여)님의 2015년 8월 30일 (일) 01:52 판 (→‎삭제(Removal): 깔끔한 해석을 위해, 노드 삭제 시 자식 1개를 보유한 노드인 상황만을 고려해야 하는 이유를 자세하게 설명하였음.)

레드-블랙 트리는 자가 균형 이진 탐색 트리(self-balancing binary search tree)로써, 대표적으로는 연관 배열 등을 구현하는 데 쓰이는 자료구조이다. 최초의 구조는 1972년 루돌프 바이어가 창안했으며, 이를 "대칭형 이진 B-트리"라고 불렀고, 1978년 레오 귀바스(Leo J. Guibas)와 로버트 세지윅이 발표한 논문에서 레드-블랙 트리라는 이름이 등장하게 되었다. 레드-블랙 트리는 복잡한 자료구조이지만, 실 사용에서 효율적이고, 최악의 경우에도 상당히 우수한 실행 시간을 보인다: 트리에 n개의 원소가 있을 때 O(log n) 의 시간복잡도로 삽입, 삭제, 검색을 할 수 있다.

용어

레드-블랙 트리는 이진 트리의 특수한 형태로써, 컴퓨터 공학 분야에서 숫자 등의 비교 가능한 자료를 정리하는 데 쓰이는 자료구조이다. 이진 트리에서는 각각의 자료가 '노드(node, 분기점)'에 저장이 된다. 자료를 트리 구조로 저장할 때, 노드들 중 최상위에 잇는 노드를 루트 노드라고 부른다. 이진 트리에서 노드는 자신과 연결되는 최대 두 개의 자식 노드를 가질 수 있다. 각각의 자식 노드도 역시 자신과 연결되는 최대 두 개의 자식 노드를 가질 수 있으며, 이런식으로 계속 연결된다. 그러므로, 어떤 트리도 그 트리의 루트 노드로부터 그 트리에 속한 모든 노드에 도달할 수 있다.

어떤 노드에 자식 노드가 없다면, 그 노드를 리프 노드라고 부르는데, 이는 그 노드가 말 그대로 트리의 맨 가장자리에 있기 때문이다. 트리의 노드 중 하나를 루트 노드로 하고 그 자신과 자식 노드들로 이루어진 트리도 동일하게 트리 구조를 가지는데, 이를 부분 트리(sub-tree)라고 한다. 레드-블랙 트리에서는 리프 노드들은 비어있고, 자료를 가지고 있지 않다.

레드-블랙 트리를 포함한 이진 탐색 트리는, 모든 노드에 대해 '자신이 가진 자료는 자신보다 오른쪽에 위치한 부분트리가 가지고 있는 모든 자료보다 작거나 같고, 자신보다 왼쪽에 위치한 부분트리가 가지고 있는 모든 자료보다 크거나 같다' 라는 조건을 만족한다. 이런 특성 때문에 특정 값을 빠르게 찾아 낼 수 있으며, 각 구성원소(elements)간의 효율적인 in-order traversal이 가능하다.

용도와 장점

레드-블랙 트리는 자료의 삽입과 삭제, 검색에서 최악의 경우에도 일정한 실행 시간을 보장한다(worst-case guarantees). 이는 실시간 처리와 같은 실행시간이 중요한 경우에 유용하게 쓰일 뿐만 아니라, 일정한 실행 시간을 보장하는 또 다른 자료구조를 만드는 데에도 쓸모가 있다. 예를 들면, 각종 기하학 계산에 쓰이는 많은 자료 구조들이 레드-블랙 트리를 기반으로 만들어져 있다.

AVL 트리는 레드-블랙 트리보다 더 엄격하게 균형이 잡혀 있기 때문에, 삽입과 삭제를 할 때 최악의 경우에는 더 많은 회전(rotations)이 필요하다.

레드-블랙 트리는 함수형 프로그래밍에서 특히 유용한데, 함수형 프로그래밍에서 쓰이는 연관 배열이나 집합(set)등을 내부적으로 레드-블랙 트리로 구현해 놓은 경우가 많다. 이런 구현에는 삽입, 삭제시 O(log n)만큼의 시간이 필요하다.

레드-블랙 트리는 2-3-4 트리와 등장변환이 가능하다(isometry). 다시 말해서, 모든 2-3-4 트리에는 구성 원소와 그 순서(order)가 같은 레드-블랙 트리가 최소한 하나 이상 존재한다는 말이다. 2-3-4 트리에서의 삽입, 삭제 과정은 레드-블랙 트리에서의 색 전환(color-flipping)과 회전(rotation)과 같은 개념이다. 그러므로 2-3-4 트리는 레드-블랙 트리의 동작 과정(logic)을 이해하는 데 많은 도움을 주며, 이런 이유로 많은 알고리즘 교과서들이 실제로는 잘 쓰이지 않음에도 불구하고 2-3-4 트리를 레드-블랙 트리가 나오기 바로 전에 소개하고 있다.

특성(Properties)

레드-블랙 트리의 예

레드-블랙 트리는 각각의 노드가 레드 나 블랙 인 색상 속성을 가지고 있는 이진 탐색 트리이다. 이진 탐색 트리가 가지고 있는 일반적인 조건에 다음과 같은 추가적인 조건을 만족해야 유효한(valid) 레드-블랙 트리가 된다: [1]

  1. 노드는 레드 혹은 블랙 중의 하나이다.
  2. 루트 노드은 블랙이다.
  3. 모든 리프 노드는 블랙이다.
  4. 레드 노드의 자식노드 양쪽은 언제나 모두 블랙이다. (즉, 레드 노드는 연달아 나타날 수 없으며, 블랙 노드만이 레드 노드의 부모 노드가 될 수 있다)
  5. 어떤 노드로부터 시작되어 리프 노드에 도달하는 모든 경로에는 리프 노드를 제외하면 모두 같은 개수의 블랙 노드가 있다.

위 조건들을 만족하게 되면, 레드-블랙 트리는 가장 중요한 특성을 나타내게 된다: 루트 노드부터 가장 먼 경로까지의 거리가, 가장 가까운 경로까지의 거리의 두 배 보다 항상 작다. 다시 말해서 레드-블랙 트리는 개략적(roughly)으로 균형이 잡혀 있다(balanced). 따라서, 삽입, 삭제, 검색시 최악의 경우(worst-case)에서의 시간복잡도가 트리의 높이(또는 깊이)에 따라 결정되기 때문에 보통의 이진 검색 트리에 비해 효율적이라고 할 수 있다.

왜 이런 특성을 가지는지 설명하기 위해서는, 네 번째 속성에 따라서, 어떤 경로에도 레드 노드가 연이어 나타날 수 없다는 것만 알고 있어도 충분하다. 최단 경로는 모두 블랙 노드로만 구성되어 있다고 했을 때, 최장 경로는 블랙 노드와 레드 노드가 번갈아 나오는 것이 될 것이다. 다섯 번째 속성에 따라서, 모든 경로에서 블랙 노드의 수가 같다고 했기 때문에 존재하는 모든 경로에 대해 최장 경로의 거리는 최단 경로의 거리의 두배 이상이 될 수 없다.

트리 구조를 나타낼 때, 어떤 노드는 자식(child)를 하나만 가질 수도 있고, leaf node는 데이터를 담고 있을 수 있다. 레드-블랙 트리도 이와 같은 방법으로 나타내 볼 수도 있지만, 그런 표현 방식으로는 레드-블랙 트리의 특성이 변하게 되고, 알고리즘과 상충되게 나타날 수 있다. 그래서, 이 문서에서는 "nil leaves" 나 "null leaves"를 사용하고 있는데, 이 "null leaf"는 위의 그림에서와 같이 자료를 가지고 있지 않으며, 트리의 끝을 나타내는 데만 쓰인다. 트리 구조를 그림으로 표현할 때, 종종 이 "null leaf"를 생략하고 그리는 경우가 많은데, 그렇게 되면 그림상으로는 레드-블랙 트리의 특성을 만족하지 못하는 것처럼 보일 수 있으나 실제로는 그렇지 않다. 이렇게 함으로써, 모든 노드들은 설령 하나 또는 두개의 자식이 "null leaf" 일지라도, 두개의 자식(children)을 가지게 된다.

간혹 레드-블랙 트리를 노드가 아닌 붉은색 또는 검은색 선분(edge)으로 설명하기도 하는데, 실제로는 같은 이야기이다. 어떤 노드의 색은 노드와 그 부모를 연결하는 선분의 색에 대응되기 때문인데, 차이점이 있다면 레드-블랙 트리의 두 번째 속성에서 언급된 root node가 선분으로 설명할 경우 존재하지 않는다는 점이다.

동작

레드-블랙 트리의 읽기 전용(read-only) 동작(검색 등)은 이진 탐색 트리의 읽기 전용 동작의 구현을 변경하지 않아도 되는데, 이는 레드-블랙 트리가 이진 탐색 트리의 특수한 한 형태이기 때문이다. 그러나 삽입(insertion)과 삭제(removal)의 경우 이진 탐색 트리의 구현에 따른 동작만으로는 레드-블랙 트리의 특성을 만족하지 못하게 된다. 레드-블랙 트리의 특성을 다시 만족하게 만들기 위해서는 O(log n) 또는 amortized O(1)번의 색 변환과(실제로는 매우 빨리 이루어진다) 최대 3회의 트리 회전(tree rotation)이 필요하다(삽입의 경우 2회). 삽입과 삭제는 복잡한 동작이지만, 그 복잡도는 여전히 O(log n)이다.

삽입(Insertion)

레드-블랙 트리의 삽입은 단순 이진 탐색 트리에서 하는 것과 같이 노드를 삽입하고, 색을 붉은색으로 정하는 것으로 시작한다. 그 다음 단계는, 그 주위 노드의 색에 따라 달라진다. 여기서 '삼촌 노드' 라는 것을 도입할텐데, 이는 같은 높이에 있는 옆 노드(다시 말해, 사촌)의 부모 노드(삼촌)를 뜻한다. 여기서 레드-블랙 트리의 특성이 추가된다 :

  • 특성 3(null node를 포함한 모든 leaf node는 검정색이다)는 언제나 변하지 않는다.
  • 특성 4(적색 노드의 모든(두) 자식은 검정색이다)는 적색 노드의 추가, 검정색 노드의 적색 노드로의 전환, 회전(rotation)에만 의해서 제대로 지켜지지 않는 상황이 된다.
  • 특성 5(어떤 노드로부터 시작되어 leaf node에 도달하는 모든 경로에는 모두 같은 개수의 블랙 노드가 있다)는 검정색 노드의 추가, 적색 노드의 검정색 노드로의 전환, 회전(rotation)에만 의해서 제대로 지켜지지 않는 상황이 된다.
주의: 삽입하는 원소를 N, N의 부모 노드를 P, P의 부모를 G, 마지막으로 N의 삼촌 노드를 U로 나타내기로 한다. 설명 도중 각 노드의 역할과 이름이 바뀌지만, 각각의 경우 노드에 붙은 이름(label)은 각 경우에 최초의 상황에서의 이름을 나타낸다. 도표에서 보여지는 색상은 각각의 경우에 예상되는 색이거나, 예상된 색에 의해 유추된 색이다.

또한 각각의 경우를 C 으로 만든 예제를 통해 보여줄 것이다. 삼촌 노드와 할아버지 노드는 다음과 같은 함수(function)에 의해 나타낼 수 있다: 

struct node *grandparent(struct node *n)
{
 if ((n != NULL) && (n->parent != NULL))
  return n->parent->parent;
 else
  return NULL;
}

struct node *uncle(struct node *n)
{
 struct node *g = grandparent(n);
 if (g == NULL)
  return NULL; // No grandparent means no uncle
 if (n->parent == g->left)
  return g->right;
 else
  return g->left;
}

첫 번째 경우

N 이라고 하는 새로운 노드가 트리의 시작(root)에 위치한다. 이 경우, 레드-블랙 트리의 첫 번째 속성(트리의 시작은 검정색이다)을 만족하기 위해서, N을 검정색으로 표시한다. 이 경우, 시작점으로부터 뻗어나가는 모든 경로에 검정색 노드를 하나 추가한 셈이 되기 때문에 레드-블랙 트리의 다섯 번째 속성(한 노드에서부터 뻗어나가는 모든 경로에 대해 검정색 노드의 수는 같다)은 여전히 유효하다. 

void insert_case1(struct node *n)
{
 if (n->parent == NULL)
  n->color = BLACK;
 else
  insert_case2(n);
}

두 번째 경우

새로운 노드의 부모 노드 P가 검정색이므로, 레드-블랙 트리의 네 번째 속성(붉은색 노드의 모든 자식 노드는 검정색이다)은 유효하다. 그러므로 두 번째 경우에도 이 트리는 적절한 레드-블랙 트리이다. 레드-블랙 트리의 다섯 번째 속성(한 노드에서부터 뻗어나가는 모든 경로에 대해 검정색 노드의 수는 같다)도 별 문제가 없는데, 이는 새로운 노드 N은 두개의 검정색 노드를 leaf node로 가지고 있기 때문이다. 비록 N이 붉은색 노드라고 해도 N이 들어간 자리에 원래 위치했던 노드의 색이 검정색이었으므로, N의 자식 노드에게서 시작되는 경로들은 모두 같은 수의 검정색 노드를 가지게 되고, 결과적으로 다섯 번째 속성은 유지되게 된다. 

void insert_case2(struct node *n)
{
 if (n->parent->color == BLACK)
  return; /* Tree is still valid */
 else
  insert_case3(n);
}
주의: 위의 경우, N은 할아버지 노드 G를 가지고 있다고 가정해도 되는데, N의 부모 노드가 붉은색이라면 그 부모 노드가 root node가 될 수 없고, 붉은색 노드의 부모 노드는 검정색 노드 밖에 될 수 없기 때문이다.

또한 N은 삼촌 노드가 있다고 가정할 수 있는데, 위의 네 번째, 다섯 번째 노드에서는 leaf node에 해당한다.

세 번째 경우

세 번째 경우의 도식

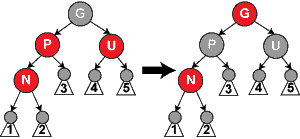
만약 부모 노드 P와 삼촌 노드 U가 모두 붉은색 노드라면, 레드-블랙 트리의 다섯 번째 속성(한 노드에서부터 뻗어나가는 모든 경로에 대해 검정색 노드의 수는 같다)을 유지하기 위해서, P와 U를 모두 검정색으로 바꾸고 할아버지 노드 G를 붉은색으로 바꾼다. 이렇게 함으로써 붉은색 노드인 N은 검정색 부모 노드를 가지게 된다. 그런데 이번에는 할아버지 노드 G가 레드 블랙 트리의 두 번째 속성(root node는 검정색이다)이나 네 번째 속성(붉은색 노드의 두 자식 노드는 검정색이다)을 만족하지 않을 수 있다(네 번째 속성은 G의 부모 노드가 붉은색일 경우 만족하지 않는다). 이를 해결하기 위해서 G에 대해 지금까지 설명한 첫 번째 경우부터 세 번째 경우까지를 재귀적으로(recursively) 적용한다. 이 작업은 삽입 과정 중에 발생하는 유일한 재귀 호출(recursive call)이며, 회전(rotation) 작업을 하기 전에 적용해야 한다는 것에 주의한다.(이는 일정한 횟수의 회전 작업만이 필요하다는 것을 증명한다.) 

void insert_case3(struct node *n)
{
 struct node *u = uncle(n), *g;

 if ((u != NULL) && (u->color == RED)) {
  n->parent->color = BLACK;
  u->color = BLACK;
  g = grandparent(n);
  g->color = RED;
  insert_case1(g);
 } else {
  insert_case4(n);
 }
}
주의: 이 후의 단계에서는 부모 노드 P가 할아버지 노드 G의 왼쪽 자식이라고 가정하고 진행하도록 한다. 만약 P가 G의 오른쪽 자식이라고 했을 때는 네 번째, 다섯 번째 경우에서 왼쪽과 오른쪽을 바꿔서 진행하면 된다. 소스 코드에서는 이를 이미 고려해서 작성되었다.

네 번째 경우

네 번째 경우의 도식

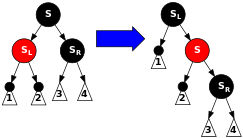
부모 노드 P가 붉은색인데, 삼촌 노드 U는 검정색이다; 또한 새로운 노드 N은 P의 오른쪽 자식 노드이며, P는 할아버지 노드 G의 왼쪽 자식 노드이다. 이 경우, N과 P의 역할을 변경하기 위해서 왼쪽 회전을 하게 된다; 그 후, 부모 노드였던 P를 다섯 번째 경우에서 처리하게 되는데, 이는 레드-블랙 트리의 네 번째 속성(붉은색 노드의 모든 자식은 검정색 노드이다)을 아직 만족하지 않기 때문이다. 회전 작업은 몇몇 경로들[2]이 이전에는 지나지 않았던 노드를 지나게 하는데, 그럼에도 양쪽 노드가 모두 붉은색이므로, 레드-블랙 트리의 다섯 번째 속성(한 노드에서부터 뻗어나가는 모든 경로에 대해 검정색 노드의 수는 같다)을 위반하지 않는다. 

void insert_case4(struct node *n)
{
 struct node *g = grandparent(n);

 if ((n == n->parent->right) && (n->parent == g->left)) {
  rotate_left(n->parent);
  n = n->left; 
 } else if ((n == n->parent->left) && (n->parent == g->right)) {
  rotate_right(n->parent);
  n = n->right; 
 }
 insert_case5(n);
}

static void rotate_left(struct node *n)
{
 struct node *c = n->right;
 struct node *p = n->parent;

 if (c->left != NULL)
  c->left->parent = n;

 n->right = c->left;
 n->parent = c;
 c->left = n;
 c->parent = p;

 if (p != NULL) {
  if (p->left == n)
   p->left = c;
  else
   p->right = c;
 }
}

static void rotate_right(struct node *n)
{
 struct node *c = n->left;
 struct node *p = n->parent;

 if (c->right != NULL)
  c->right->parent = n;

 n->left = c->right;
 n->parent = c;
 c->right = n;
 c->parent = p;

 if (p != NULL) {
  if (p->right == n)
   p->right = c;
  else
   p->left = c;
 }
}

다섯 번째 경우

다섯 번째 경우의 도식

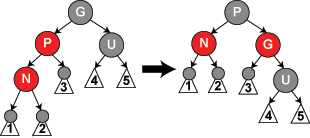
부모 노드 P는 붉은색이지만 삼촌 노드 U는 검정색이고, 새로운 노드 N이 P의 왼쪽 자식 노드이고, P가 할아버지 노드 G의 왼쪽 자식 노드인 상황에서는 G에 대해 오른쪽 회전을 한다. 회전의 결과 이전의 부모 노드였던 P는 새로운 노드 N과 할아버지 노드 G를 자식 노드로 가지게 된다. G가 이전에 검정색이었고, P는 붉은색일 수밖에 없기 때문에, P와 G의 색을 반대로 바꾸면 레드-블랙 트리의 네 번째 속성(붉은색 노드의 두 자식 노드는 검정색 노드이다)을 만족하게 된다. 레드-블랙 트리의 다섯 번째 속성(한 노드에서부터 뻗어나가는 모든 경로에 대해 검정색 노드의 수는 같다)은 계속 유지되는데, 이는 이전에 P를 포함하는 경로는 모두 G를 지나게 되고, 바뀐 후 G를 포함하는 경로는 모두 P를 지나게 되기 때문이다. 바뀌기 전에는 G가, 바뀐 후에는 P가 P, G, N중 유일한 검정색 노드이다. 

void insert_case5(struct node *n)
{
 struct node *g = grandparent(n);

 n->parent->color = BLACK;
 g->color = RED;
 if (n == n->parent->left)
  rotate_right(g);
 else
  rotate_left(g);
}

삽입 동작은 치환 작업인데, 이는 모든 호출(call)이 tail recursion이기 때문이다.

삭제(Removal)

통상적인 이진검색트리에서 두 개의 non-leaf 자식을 가진 노드를 지울 때, 우리는 노드의 왼쪽 서브트리에서 최대값(중위 순회시 바로 전값)을 찾거나, 오른쪽 서브트리에서 최소값(중위 순회시 바로 뒤에 값)을 찾아 해당 값을 지우고자 하는 노드로 옮긴다.(여기에서 처럼) 그리고 나서 우리는 값을 복사해온 노드를 지우는데, 이 노드는 반드시 2개보다 적은 non-leaf 자식을 갖고 있다. ('자식'이 아니라 'non-leaf 자식'이라고 표현한 이유는 일반적인 이진검색트리와는 달리, 레드-블랙 트리의 노드는 leaf 노드가 어디든 붙을 수 있기 때문이다. 따라서, 모든 노드들은 두 개의 자식 노드를 가진 내부 노드이거나 자식을 하나도 가지지 않은 leaf노드가 될 수밖에 없다. 실질적으로, 레드-블랙 트리에서 두 개의 leaf 자식을 가진 내부 노드들은 이진검색트리에서의 일반적인 leaf 노드와 같다.) 단순 값을 복사하는 것은 레드-블랙 특성(properties)을 위반하지 않는다. 문제가 되는 부분은 삭제한 노드의 주변 노드가 특성을 위반하는지의 여부이다. 참고로 알아두어야 할 점은, 이진 검색 트리에서 삭제를 수행할 때에는 앞서 말했듯 왼쪽 서브트리에서의 최대값이나, 오른쪽 서브트리에서의 최소값을 삭제한 노드의 위치에 삽입한다는 것. 이 때, 삭제한 노드를 대체할 노드에는 반드시 1개의 자식 노드만 있다는 점이다. 그 이유는 즉슨, 자식 2개를 보유한 노드일 경우, 왼쪽 자식 < 대체 노드 < 오른쪽 자식이라는 결론이 도출되므로, 자식 2개를 보유할 가능성은 절대적으로 0이라는 것이다. 이와 같은 까닭으로, 삭제는 최대 한 개의 non-leaf 자식을 갖고 있는 노드를 삭제하는 문제로 치환할 수 있다. 따라서, 우리가 이 문제의 해법을 찾고 나면, 이 해법은 최대 한 개의 non-leaf 자식을 가진 노드를 지우는 문제 뿐 아니라 두 개의 non-leaf 자식을 가진 노드를 지우는 문제까지도 적용할 수 있다.

그러므로, 앞으로의 논의에서 우리는 최대 한 개의 non-leaf 자식을 가진 노드를 지우는 문제에 대해서만 이야기할 것이다. M을 삭제하고자 하는 노드라 두고, C를 M의 선택된 자식이라 두자.(또한, 앞으로 M의 자식이라고도 부르겠다.) 만약 M이 non-leaf 자식을 가질 경우, 그 자식 노드를 C라고 부를 것이고, 그렇지 않은 경우 두 leaf 중 아무 노드나 자식노드 C라고 부르겠다.

만약 M이 붉은 노드이면, 우리는 단순히 특성 4에 의해 검은 노드여야 할 자식 노드 C를 M대신 치환하면 된다. (이 상황은 M이 두 개의 leaf 자식을 갖고 있을 때에만 발생한다. 왜냐하면 만약 M이 한 쪽에는 검은 non-leaf 자식 노드를 갖고 있고, 다른 쪽에 검은 leaf 자식 노드를 갖고 있다면, 양쪽의 검은 노드 갯수가 달라지게 되어 특성 5를 위반하게 되기 때문이다.) 삭제된 노드를 지나는 모든 path는 단순히 붉은 노드 하나만 없어지게 되고, 삭제된 노드의 부모와 자식 모두 검은 노드이므로, 특성 3(모든 leaf들은 검은 노드)과 특성 4(모든 붉은 노드는 두 개의 검은 자식 노드를 갖는다)는 여전히 유효하다.

또 다른 간단한 상황은 M이 검은 노드이고 C가 붉은 노드일 때이다. 검은 노드를 단순 삭제해버릴 경우 특성 4(모든 붉은 노드는 두 개의 검은 자식 노드를 갖는다)와 특성 5(특정 노드에서부터 leaf로 가는 모든 경로에서 같은 수의 검은 노드를 지난다.)를 위반할 수 있으나, 우리가 C를 검은색으로 다시 칠하면, 두 가지 특성은 모두 만족할 수 있다.

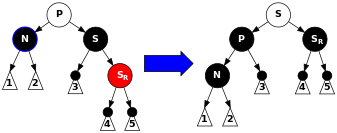
복잡한 상황은 M과 C가 모두 검은색 노드일 때이다. (이 상황은 두 개의 leaf 자식을 갖고 있는 검은 노드를 지우는 상황에서만 발생한다. 왜냐하면, 검은 노드 M이 검은색 non-leaf 자식을 한 쪽에 갖고 있고 다른 쪽에 leaf 자식을 갖고 있으면, 양 쪽의 검은 노드 갯수가 달라지게 되므로 특성 5에 대한 위반이다.) 일단, M을 자식 노드 C로 치환하자. 그리고 이 자식 노드를 N으로 다시 이름짓고, 이 노드의 형제노드(새로운 부모의 다른 자식 노드)를 S라고 이름짓자.(S는 원래 M의 형제노드이다.) 아래의 다이어그램을 보면, N의 새로운 부모를 P(M의 옛 부모)라고 표기하고, SL을 S의 왼쪽 자식, SR을 S의 오른쪽 자식(S는 leaf가 될 수 없다. 왜냐하면 만약 M과 C가 검은색이라면, M을 포함하는 P의 subtree는 2개의 검은노드-높이를 갖게되고 따라서 S를 포함하는 P의 다른 subtree 또한 2개의 검은노드 높이를 가져야만 하므로 S는 leaf 노드가 될 수 없다.

노트: 몇몇 상황에서 우리는 노드들의 이름과 역할을 바꾸고 있으나, 원래의 이름은 계속 해당 노드를 나타낸다고 보면 된다. 다이어그램에 나오는 노드의 색깔들은 해당 상황에 맞게 가정되었거나 그러한 가정을 반영하게끔 정해져있다. 흰색은 정해지지 않은 색깔이다.(빨강일 수도 있고 검정일 수도 있다.)

우리는 다음의 함수를 사용하여 형제 노드를 찾을 수 있다. 

struct node *sibling(struct node *n)
{
 if (n == n->parent->left)
  return n->parent->right;
 else
  return n->parent->left;
}
노트: 트리가 정의에 맞게끔 구성되기 위해서, 우리는 모든 변환 이후에도 모든 null leaf들이 leaf로 남겨지도록 할 것이다(leaf의 자식이 없도록). 만약 우리가 삭제하는 노드가 non-leaf(non-null) 자식 N을 갖는다면, 특성이 만족되는 것을 확인하는 것은 쉽다. 반면, N이 null leaf일 수 있는데, 이 경우에도 모든 상황을 만족시킬 수 있다는 것을 다이어그램(혹은 코드)를 통해 증명하겠다.

우리는 다음의 코드를 통해 위에서 소개한 단계를 밟아나갈 수 있다. 여기서 replace_node함수는 child를 n의 자리에 대입하는 함수이다. 편의를 위해서, 이 섹션의 코드들은 null leaf들은 NULL 대신 실제 노드 객체로 표현할 것이라는 가정을 바탕에 두고 있다.(삽입섹션에서 사용된 코드들은 양쪽 표현을 다 사용했었다.) 

void delete_one_child(struct node *n)
{
 /*
  * 선제조건: n이 최대 하나의 non-null 자식을 갖고 있음.
  */
 struct node *child = is_leaf(n->right) ? n->left : n->right;

 replace_node(n, child);
 if (n->color == BLACK) {
  if (child->color == RED)
   child->color = BLACK;
  else
   delete_case1(child);
 }
 free(n);
}
노트: 만약 N이 null leaf이이고 우리가 null leaf들을 실제 노드 객체로 치환하고자 하지 않는다면, 알고리즘에서 delete_case1()을 부모노드(우리가 지우고자 하는 노드, 위의 코드에서 n)에 먼저 호출해주고 원래 노드를 뒤에 삭제하면 된다. 이 방식은 부모가 검은색이기 때문에 null leaf처럼 사용할 수 있으므로(그리고 이는 '유령' leaf로 불리기도 한다.) 가능하다. 그리고 우리는 n이 위에서 보듯이 모든 동작을 수행한 후 leaf로 남아있을 것이기 때문에 안전하게 마지막 부분에서 이 노드를 삭제할 수 있다.

만약 N과 N의 원래 부모가 둘 다 검정이었다면, 부모를 삭제하는 것은 N을 지나는 path가 검은 노드 한 개를 덜 갖게 되므로 해서는 안된다. 이는 특성 5(특정 노드에서부터 leaf로 가는 모든 경로에서 같은 수의 검은 노드를 지난다.)를 위반하기 때문에, 트리는 재균형을 맞춰주어야 한다. 고려해보아야 할 몇몇 상황들이 있다:

Case 1: N 이 새로운 루트가 될때. 이 경우에는 더 할게 없다. 우리는 모든 경로에서 하나의 검은 노드를 삭제했고, 새로운 루트 노드는 검은색이므로 모든 특성이 보존된다. 

void delete_case1(struct node *n)
{
 if (n->parent != NULL)
  delete_case2(n);
}
Note: cases 2, 5, 그리고 6에서, N을 P의 왼쪽 자식노드라고 가정하겠다. 만약 N이 오른쪽 자식 노드라면, 이 세 가지 case에서 '왼쪽'과 '오른쪽'을 바꾸면 된다. 다시 한 번 밝히지만, 코드예제에서는 두 가지 상황을 모두 고려했다.
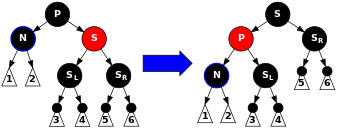Diagram of case 2
Diagram of case 2

Case 2: S 가 빨강일 경우. 이 경우 P와 S의 색을 바꾸고, P에서 왼쪽으로 회전하면, S가 N의 할아버지 노드가 된다. P는 빨간색 자식 노드가 있을 경우, 검은색이 되어야 한다. 비록 모든 경로에서 같은 수의 검은색 노드들이 있지만, 이제 N이 검은색 형제노드와 붉은색 부모 노드를 갖고 있으므로, 스텝 4,5, 또는 6으로 진행할 수 있다.(새로운 형제노드는 붉은색 S노드의 자식노드이었던 노드이므로 검은색 노드이다.) 이후의 case들에서 우리는 N의 새로운 형제노드를 S로 표기하겠다. 

void delete_case2(struct node *n)
{
 struct node *s = sibling(n);

 if (s->color == RED) {
  n->parent->color = RED;
  s->color = BLACK;
  if (n == n->parent->left)
   rotate_left(n->parent);
  else
   rotate_right(n->parent);
 }
 delete_case3(n);
}
Diagram of case 3
Diagram of case 3

Case 3: P, S, 그리고 S의 자식들이 검은색인 경우. 이 경우, 우리는 간단히 S를 빨강으로 칠하면 된다. 그 결과, S를 지나는 모든 경로들(N을 지나지 않는 경로)은 하나의 검은노드를 적게 갖고 있게 된다. 하지만, N의 원래 부모노드를 삭제하는 과정에서 N을 지나는 모든 경로들은 하나의 검은 노드를 적게 갖게 되므로, 양쪽은 같은 수의 검은 노드를 갖게 된다. 그러나, P를 지나는 모든 경로들은 P를 지나지 않는 모든 경로에 대해 검은 노드를 한 개 적게 지니게 되므로, 특성 5(특정 노드에서부터 leaf로 가는 모든 경로에서 같은 수의 검은 노드를 지난다.)를 위반하게 된다. 이를 바로잡기 위해서, 우리는 P에다 case 1부터 시작하는 rebalancing 과정을 수행해야 한다. 

void delete_case3(struct node *n)
{
 struct node *s = sibling(n);

 if ((n->parent->color == BLACK) &&
     (s->color == BLACK) &&
     (s->left->color == BLACK) &&
     (s->right->color == BLACK)) {
  s->color = RED;
  delete_case1(n->parent);
 } else
  delete_case4(n);
}
Diagram of case 4
Diagram of case 4

Case 4: S와 S의 자식들은 검은색이지만, P는 빨강인 경우. 이 경우, 우리는 단순히 S와 P의 색을 바꾸면 된다. 이는 S를 지나는 경로의 검은 노드 갯수에 영향을 주지 않지만, N을 지나는 경로에 대해서는 검은 노드의 갯수를 1개 증가시킨다. 이는 원래 삭제된 검은 노드의 갯수를 보충해준다. 

void delete_case4(struct node *n)
{
 struct node *s = sibling(n);

 if ((n->parent->color == RED) &&
     (s->color == BLACK) &&
     (s->left->color == BLACK) &&
     (s->right->color == BLACK)) {
  s->color = RED;
  n->parent->color = BLACK;
 } else
  delete_case5(n);
}
Diagram of case 5
Diagram of case 5

Case 5: S가 검정, S의 왼쪽 자식이 빨강, S의 오른쪽 자식이 검정이며, N이 부모의 왼쪽 자식인 경우. 이 경우 우리는 S를 오른쪽으로 회전시켜서 S의 왼쪽 자식이 S의 부모노드이자 N의 새로운 형제 노드가 되도록 만든다. 그리고 나서 우리는 S의 색을 부모 노드의 색깔과 바꾼다. 모든 경로는 여전히 같은 수의 검은 노드수를 가지나, 이제 N이 오른쪽에 붉은 노드를 자식으로 둔 검은색 형제노드를 갖게 되었으므로, 6번째 case로 진행하면 된다. N이나 N의 부모노드는 이 변형에 아무런 영향을 받지 않는다. (다시 말하지만, N의 새로운 형제 노드를 6번째 case에서 S라고 부르도록 할 것이다.) 

void delete_case5(struct node *n)
{
 struct node *s = sibling(n);

 if  (s->color == BLACK) { /* 이 문은 자명하다,
case 2로 인해서(case 2에서 '''N'''의 형제 노드를 원래 형제 노드 '''S'''의 자식노드로 바꾸지만,
빨강 부모노드는 빨강 자식 노드를 가질 수 없기 때문에 '''N'''의 새로운 형제노드는 빨강일 수 없다). */
/* 다음의 문은 빨강을 '''N'''의 부모노드의 오른쪽 자식의 오른쪽 자식으로 두기 위함이다.
   혹은 '''N'''의 부모노드의 왼쪽 자식의 왼쪽 자식으로 두기 위함. case 6에 넘기기 위해 */
  if ((n == n->parent->left) &&
      (s->right->color == BLACK) &&
      (s->left->color == RED)) { /* this last test is trivial too due to cases 2-4. */
   s->color = RED;
   s->left->color = BLACK;
   rotate_right(s);
  } else if ((n == n->parent->right) &&
             (s->left->color == BLACK) &&
             (s->right->color == RED)) {/* this last test is trivial too due to cases 2-4. */
   s->color = RED;
   s->right->color = BLACK;
   rotate_left(s);
  }
 }
 delete_case6(n);
}
Diagram of case 6
Diagram of case 6

Case 6: S가 검은색, S의 오른쪽 자식이 빨강이며, N 이 P의 왼쪽 자식인 경우. 이 경우 우리는 P를 왼쪽으로 회전해서, S가 P와 S의 오른쪽 자식노드의 부모 노드가 되게 하한다. 그리고나서, 우리는 P와 S의 색을 바꾸고, S의 오른쪽 자식노드를 검은색으로 만든다. 이 subtree는 루트노드가 회전하기 전과 마찬가지로 여전히 같은 색을 지니므로 특성 4(모든 빨강 노드는 두개의 검은 노드를 자식으로 갖는다)와 특성 5(특정 노드에서부터 leaf로 가는 모든 경로에서 같은 수의 검은 노드를 지난다.)에 위배되지 않는다. 그러나, N은 이제 하나의 추가적인 검은 조상 노드를 가지게 된다:P가 검은색으로 바뀌든가, 아니면 P가 검은색이었고 S가 검은색 할아버지 노드로 추가되었든지. 그러므로, N을 지나는 경로는 하나의 추가적인 검은 노드를 갖게 된다.

반면, N을 통과하지 않으면, 두 가지의 경우가 존재한다:

  • N의 새로운 형제노드를 지나는 경우. 이 경우, 경로는 S와 P를 지나고, 변형되기 전이나 후에나, 단지 달라진 색과 장소만 지날 뿐이다. 그러므로 경로는 같은 수의 검은 노드를 지난다. (그림에서 3번 경로)
  • N의 새로운 삼촌노드를 지나는 경우. 이 경우, 변형되기 전 S의 부모노드, S 그리고 S의 오른쪽 자식노드(원래 빨강이었던)를 지나는 경로였으나, 변형 후에는 S(변형전 부모노드의 색을 갖게된)와 S의 오른쪽 자식노드(빨강에서 검정으로 색이 바뀐)를 지나는 경로로 바뀐다. 결과적으로 이 두 경로는 같은 수의 검은 노드를 지난다.(그림에서 4,5번 경로)

어떤 경우든, 검은 노드의 갯수는 변화하지 않는다. 그러므로, 우리는 특성 4와 특성 5를 복원할 수 있다. 그림에서 하얀색 노드는 검정이나 빨강 모두가 될 수 있으나, 변형 전과 후에 같은 색을 가리키게 된다. 

void delete_case6(struct node *n)
{
 struct node *s = sibling(n);

 s->color = n->parent->color;
 n->parent->color = BLACK;

 if (n == n->parent->left) {
  s->right->color = BLACK;
  rotate_left(n->parent);
 } else {
  s->left->color = BLACK;
  rotate_right(n->parent);
 }
}

case 2를 통과하면 N과 S는 반드시 검은색 노드가 된다. case 2를 통과한 후에 남는 경우의 수는 아래와 같은데, 아래의 경우 모두 각각의 case에서 해결된다. (P, SL, SR) = (검,검,검) - case 3에서 해결, (빨,검,검) - case 4에서 해결, (검,빨,검) - case 5에서 해결, (빨,빨,검) - case 5에서 해결, (검,검,빨) - case 6에서 해결, (빨,검,빨) - case 6에서 해결, (검,빨,빨) - case 6에서 해결, (빨,빨,빨) - case 6에서 해결. case 1-6까지의 경우를 다 지나면 위와 같이 모든 경우의 수에 대해 커버됨을 확인할 수 있다. (역자 주)

다시 이야기하지만, 함수 콜은 모두 tail recursion을 이용하므로, 알고리즘은 in-place이다. 위의 알고리즘에서, 부모 노드에 대해 case 1으로 재귀하는 delete case 3을 제외하고는 모든 case에 대해 순서대로 chained되어 있다: 이 경우가 in-place 구현에서 유일하게 효과적으로 루프를 도는 case이다.(case 3에서 한 번의 회전 이후)

추가적으로, 자식 노드에 대해서는 tail recursion이 일어나지 않으므로, tail recursion 루프는 자식 노드에서부터 연결된 조상 노드들로 거꾸로 올라간다. case 1로 돌아가는 루프는 O(log n)번을 넘지 않는다.(n은 삭제 전에 트리에 존재하는 모든 노드의 갯수) 만약 case 2에서 회전이 일어나면(case 1-3 루프 중에 유일한 회전), N의 부모노드는 회전 후 빨강으로 변하고, 루프에서 빠져나온다. 그러므로 이 루프 내에서는 회전은 기껏해야 한 번 있다. 루프를 빠져나오고 나서는 두 번 보다 많은 횟수의 추가적인 회전은 일어나지 않기 때문에 모두 합쳐서 3번보다 많은 수의 회전은 일어나지 않는다.

Proof of asymtotic bounds

{빈문서}

병렬 알고리즘(Parallel algorithms)

아이템의 수에 비례하여 컴퓨터 프로세서를 이용할 수 있다면, 정렬되어 있는 아이템을 가지고 레드-블랙 트리를 만드는 병렬 알고리즘은 상수시간이나 시간으로 구현될 수 있다. 빠른 검색, 삽입, 삭제를 위한 병렬 알고리즘 또한 알려져 있다.[3]

각주

  1. ↑ en:Thomas H. Cormen; Charles E. Leiserson; Ronald L. Rivest; en:Clifford Stein (2009). 《Introduction to Algorithms (3rd ed.)》. MIT Press. 308-309쪽. ISBN 978-0-262-03384-8. 
  2. ↑ "1" 이라는 이름이 붙어 있는 부분 트리(sub-tree)
  3. ↑ Park, Heejin; Park, Kunsoo (2001). “Parallel algorithms for red–black trees”. 《Theoretical computer science》 (Elsevier) 262 (1–2): 415–435. doi:10.1016/S0304-3975(00)00287-5. Our parallel algorithm for constructing a red–black tree from a sorted list of n items runs in O(1) time with n processors on the CRCW PRAM and runs in O(log log n) time with n / log log n processors on the EREW PRAM. 
원본 주소 "https://ko.wikipedia.org/w/index.php?title=레드-블랙_트리&oldid=14725072"