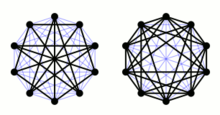
 페테르센 그래프(左)와 그 여 그래프(右)
페테르센 그래프(左)와 그 여 그래프(右)
그래프 이론에서 여 그래프(餘graph, 영어: complement graph)는 임의의 그래프에서 두 점이상의 경우 이들 사이에 변이 존재하면 변을 제거하고, 변이 없었으면 변이 추가되는 일대일 대응하는 그래프이다.
그래프  의 여 그래프
의 여 그래프  는 다음과 같다.
는 다음과 같다.


여 그래프의 여 그래프는 원래 그래프이다.

그래프의 독립집합은 여 그래프의 클릭에 대응한다.
스스로의 여 그래프와 동형인 그래프를 자기 여 그래프(영어: self-complementary graph)라고 한다.  개의 꼭짓점을 갖는 자기 여 그래프의 수는 다음과 같다 (
개의 꼭짓점을 갖는 자기 여 그래프의 수는 다음과 같다 ( ).
).
- 1, 0, 0, 1, 2, 0, 0, 10, 36, 0, 0, 720, … (OEIS의 수열 A000171)
예를 들어, 다음과 같은 그래프들이 자기 여 그래프이다.
- 자명 그래프

- 경로 그래프

- 순환 그래프

- 라도 그래프
가능한 변의 수  가 짝수여야 하므로, 유한 자기 여 그래프의 꼭짓점의 수는
가 짝수여야 하므로, 유한 자기 여 그래프의 꼭짓점의 수는  이다.
이다.
외부 링크[편집]













