비음수 행렬 분해

음수 미포함 행렬 분해(Non-negative matrix factorization, NMF)는 음수를 포함하지 않은 행렬 V를 음수를 포함하지 않은 행렬 W와 H의 곱으로 분해하는 알고리즘이다. 행렬이 음수를 포함하지 않는 성질은 분해 결과 행렬을 찾기 쉽게 만든다. 일반적으로 행렬 분해는 정확한 해가 없기 때문에 이 알고리즘은 대략적인 해를 구하게 된다. 음수 미포함 행렬 분해는 컴퓨터 시각 처리, 문서 분류, 음파 분석, 계량분석화학, 추천 시스템 등에 쓰인다.

NMF

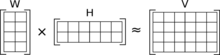
|음수 미포함 행렬 분해: 행렬 V가 행렬 W와 행렬 H의 곱으로 근사된다.

역사

계량분석화학에서 자기 모델링 그래프 분해라는 이름으로 오랫동안 행해져 왔다. 이 경우 오른쪽 행렬에 있는 벡터들은 떨어져 있는 값보다는 연속적인 값을 갖게 된다. 또 한 핀란드의 연구자들은 양수 행렬 분해라는 이름으로 1990년대 중에 이 알고리즘을 연구해왔다. 연구자 Lee와 Seung이 이 분해의 성질과 두 개의 간단한 분해 알고리즘을 음수 미포함 행렬 분해로 소개한 뒤 널리 알려졌다.

동기

예를 들어

• 10000x500 크기의 단어들을 포함한 행렬 V가 있다고 하자. V의 500개의 열(벡터)은 문서를 나타낸다.

• 이 행렬 V를 10000x10과 10x500의 크기를 가지는 W와 H로 분해했다고 하자. W는 10개의 열을 가지고 있는 행렬이다.

• V=WH이기 때문에 행렬 V는 W의 선형 결합으로 나타내어지는 행렬이다. 따라서 W의 열 벡터들은 V의 특징 벡터라고 할 수 있다. 즉, V가 포함한 단어들의 특징을 분석한 행렬이 W라는 것이다.

이처럼 커다란 정보를 특징과 계수들로 어림 잡아 분해하여 정보의 특징을 파악하는 데에 쓰인다.

종류

근사적인 음수 미포함 행렬 분해

일반적으로 W의 열 개수와 H의 행 개수가 WH=V가 되도록 결정된다. 기존 행렬 V와 분해한 음수 미포함 행렬 W와 H의 곱과의 차이를 오차 U라고 이야기한다. V=WH+U. U의 원소들은 양수나 음수가 될 수 있다. W와 H의 크기가 V보다 작기 때문에 저장하거나 다루기에 용이하다. 또 V를 원래 정보보다 상대적으로 적은 정보로 표현하여 분해한 행렬 하나가 전체 정보의 대략적인 정보를 제시할 수 있다.

볼록 음수 미포함 행렬 분해

기존 음수 미포함 행렬 분해에서는 W는 어떤 행렬도 될 수 있지만 볼록 음수 미포함 행렬 분해에서는 W를 기존 입력 벡터들$(v_{1},\cdots ,v_{n})$의 볼록 결합으로 제한하기 때문에 W에 포함된 정보의 질이 크게 향상된다. 또한, 결과 행렬 H가 더 직교화되는 효과가 생긴다.

음수가 아닌 랭크 분해 (Non-negative rank factorization, NRF)

V의 음수가 아닌 랭크가 V의 랭크와 같다면 V=WH를 음수가 아닌 랭크 분해라고 한다. 음수가 아닌 랭크 분해를 찾는 것은 NP-난해이다.

여러 가지 비용 함수와 정형화 기법

어떤 비용 함수를 사용하느냐, 어떤 정형화 기법을 사용하느냐에 따라 분해의 종류가 나뉜다. 널리 쓰이는 두 가지 분해 방법에는 Lee와 Seung가 연구한 최소 제곱 오차와 양수 행렬에 대한 Kullback-Leibler 수렴 방법을 이용한 것이 있다. 두 방법은 다른 알고리즘으로 취급된다. 가장 보편적인 최소 제곱 오차를 이용한 분해를 아래에 서술한다. 다른 분해의 방법으로는 총 표준 변화를 이용한 방법이 있다. L1 정규화가 최소 제곱 오차에 같이 사용되었을 때 성긴 코딩과 형태가 유사하여 음수가 아닌 성긴 코딩이라고도 부른다.

온라인 NMF

음수 미포함 행렬 분해는 입력 데이터를 한번에 다루는 특징이 있다. 따라서 이 알고리즘은 저장하기에 너무 크거나 스트리밍과 같은 데이터에 대해서는 적용하기 힘들다. 이렇게 많은 사용자나 많은 입력이 있거나 새로운 정보가 계속 들어와 계산을 새로 해야하는 경우에는 협업 필터링을 사용할 수도 있다. 이 때 비용 함수는 같을수도 다를 수도 있지만 알고리즘은 달라져야 한다.

알고리즘

음수 미포함 행렬 $\mathbf {V}$에 근사하는 행렬곱 $\mathbf {WH}$을 찾기 위해 최신화 규칙을 반복해서 시행하면, 비용 함수의 함수값을 수렴 조건이 만족할 때까지 감소시킬 수 있고 이를 통해 구하고자 했던 분해된 행렬 $\mathbf {W}$와 $\mathbf {H}$를 얻을 수 있다. 이 때 수렴은 항상 보장된다.
즉, 알고리즘을 1) 비용 함수 2) 최신화 규칙 3) 수렴 보장으로 나누어 분석할 수 있다.

비용 함수

비용 함수에는 크게 두가지가 있다. 첫 번째 비용함수는 최소 제곱 오차로 아래 수식과 같이 표현할 수 있으며,
$F(\mathbf {A} ,\mathbf {B} )=\|\mathbf {A} -\mathbf {B} \|^{2}=\sum _{i,j}(A_{ij}-B_{ij})^{2}$
0을 하한값으로 하며 A=B일 때 하한값을 취하게 된다.

두 번째 비용함수는 B로부터 A의 발산값으로, 아래 수식과 같이 표현할 수 있다.
$D(A||B)=\sum _{i,j}(A_{ij}\log {\frac {A_{ij}}{B_{ij}}}-A_{ij}+B_{ij})$
이들 비용함수의 함수값을 최소화하는 방식을 통해, $\mathbf {V}$에 근사하는 $\mathbf {WH}$를 구한다.

최신화 규칙

각각의 비용함수들의 최신화 규칙과 그에 관한 정리는 아래와 같다.

정리 1. 아래 최신화 규칙 하에서, 최소 제곱 오차 $\|\mathbf {V} -\mathbf {WH} \|^{2}$ 는 비증가함수이다.
$H_{au}$ ← $H_{au}{\frac {(W^{T}V)_{au}}{(W^{T}WH)_{au}}}$

$W_{ia}$ ← $W_{ia}{\frac {(VH^{T})_{ia}}{(WHH^{T})_{ia}}}$
이 최신화 규칙을 통해 얻은 최소 제곱 오차가 불변할 때, W와 H는 임계점(stationary point)에 도달하게 된다. 이 명제의 역도 성립한다.

정리 2. 아래 최신화 규칙 하에서, B로부터 A의 발산값 $D(A||B)$은 비증가함수이다.
$H_{au}$ ← $H_{au}{\frac {\sum _{i}W_{ia}V_{iu}/(WH)_{iu}}{\sum _{k}W_{ka}}}$

$W_{ia}$ ← $W_{ia}{\frac {\sum _{u}H_{au}V_{iu}/(WH)_{iu}}{\sum _{v}H_{av}}}$
이 최신화 규칙을 통해 얻은 발산값이 불변할 때, W와 H는 임계점(stationary point)에 도달하게 된다. 이 명제의 역도 성립한다.

정리1과 정리2의 증명을 아래 수렴 보장성 부분에서 확인할 수 있다.

수렴 보장성

[정의]

            모든 h에 대해, 

            $G(h,h')\geq F(h),$  $G(h,h)=F(h)$  를 만족하는 $G(h,h')$를 $F(h)$의 보조 함수라고 한다.

[보조 정리1]

            G가 보조 함수일 때, 함수 F는 비증가함수이다. 즉, $h^{t+1}=argmin_{h}G(h,h^{t})$

[보조 정리2]

            행렬 $K(h^{t})$가 $K_{ab}(h^{t})=\delta _{ab}{\frac {(W^{T}Wh^{t})_{a}}{(h_{a})^{t}}}$ 를 만족하는 대각 행렬일 때, 

            $G(h,h^{t})=F(h^{t})+(h-h^{t})^{T}$▽$F(h^{t})+{\frac {1}{2}}(h-h^{t})^{T}K(h^{t})(h-h^{t})$ 

            을 만족하는 함수 $G$는 $F(h)={\frac {1}{2}}\sum _{i}(v_{i}-\sum _{a}W_{ia}h_{a})^{2}$  의 보조함수이다.

[보조 정리3]

             $G(h,h^{t})=\sum _{i}(v_{i}logv_{i}-v_{i})+\sum _{ia}W_{ia}h_{a}-\sum _{ia}v_{i}{\frac {W_{ia}(h_{a})^{t}}{\sum _{b}W_{ib}(h_{b})^{t}}}(logW_{ia}h_{a}-log{\frac {W_{ia}(h_{a})^{t}}{\sum _{b}W_{ib}(h_{b})^{t}}})$ 

             $F(h)=\sum _{i}v_{i}log({\frac {v_{i}}{\sum _{a}W_{ia}h_{a}}})-v_{i}+\sum _{a}W_{ia}h_{a}$ 일 때, 

             $G(h,h^{t})$는 $F(h)$의 보조함수이다.

정리1의 증명

보조정리1의 $G(h,h^{t})$를 보조정리2의 $G(h,h^{t})$로 바꾸면 아래와 같은 최신화 규칙을 얻는다. $h^{t+1}=h^{t}-K(h^{t})^{-1}$▽$F(h^{t})$
보조정리2의 $G(h,h^{t})$ 가 보조함수이므로, 보조정리1에 의해 함수 F는 비증가함수이다. 방정식을 풀면, $h_{a}^{t+1}=h_{a}^{t}{\frac {(W^{T}v)_{a}}{(W^{T}Wh^{t})_{a}}}$
즉, H에 대한 최신화 규칙을 유도한 것이다. 보조정리1과 보조정리2의 W와 H의 위치를 바꿔주면 W에 대한 최신화 규칙 역시 쉽게 유도할 수 있다.

정리2의 증명

보조정리3에서의 함수 $G(h,h^{t})$의 최소값을 구하기 위해 미분값을 0으로 할 때의 h값을 찾는다. ${\frac {dG(h,h^{t})}{dh_{a}}}=-\sum _{i}v_{i}{\frac {W_{ia}h_{a}^{t}}{\sum _{b}W_{ib}h_{b}^{t}}}{\frac {1}{h_{a}}}+\sum _{i}W_{ia}=0$
그러므로 $h_{a}^{t+1}={\frac {h_{a}^{t}}{\sum _{b}W_{kb}}}\sum _{i}{\frac {v_{i}}{\sum _{b}W_{ib}h_{b}^{t}}}W_{ia}$
G가 보조 함수이므로, 함수 F는 최신화를 거듭할수록 그 함수값이 감소 내지 일정하게 유지된다. 위의 식을 행렬 형식으로 바꾸면, 발산값에서의 H 최신화 규칙과 동일한 것을 알 수 있다. H와 W의 위치를 바꿔서, 발산값에서의 W의 최신화 규칙 역시 비증가함을 증명할 수 있다.

성질

정확한 음수 미포함 행렬 분해

일반적으로 음수 미포함 행렬 분해는 근사를 통해 이루어지지만, 추가적인 조건이 더해지면 정확한 행렬 분해를 얻을 수 있다.
1) 행렬 V가 자신의 계수와 같은 계수를 가진 단항 부분 행렬을 가지고 있을 때 정확한 음수 미포함 행렬 분해를 구할 수 있다.
2) 행렬 V가 대칭성을 가지고 있으며 자신의 계수와 같은 계수를 가진 대각 부분 행렬을 가지고 있을 때, 정확한 음수 미포함 행렬 분해를 구할 수 있다.
3) 행렬 W가 분리 조건을 만족하면 정확한 음수 미포함 행렬 분해를 구할 수 있다.

유일성 유무 판단

음수 미포함 행렬 분해는 유일성을 가지지 않는다. $\mathbf {WH} =\mathbf {WBB} ^{-1}\mathbf {H}$이고, 만약 새로운 행렬 $\mathbf {{\tilde {W}}=WB}$ 과 $\mathbf {\tilde {H}} =\mathbf {B} ^{-1}\mathbf {H}$ 가 음수항을 가지고 있지 않다면, 또다른 행렬 분해를 구할 수 있다.

군집 성질

음수 미포함 행렬 분해는 군집 성질을 가진다. 즉, 이 행렬 분해는 입력 자료 행렬$\mathbf {V} =(v_{1},\cdots ,v_{n})$의 행들을 무조건 군집화한다. 구체적으로, $\mathbf {V}$를 $\mathbf {V} \simeq \mathbf {W} \mathbf {H}$ 로 근사할 때 오차 함수$\min _{W,H}||V-WH||_{F},W\geq 0,H\geq 0$를 최소화하는 방식을 택한다. 만약 $HH^{T}=I$ 라는 조건이 추가된다면, 위의 최소화 과정은 K-평균 군집화의 최소화과정과 동일-음이 아니라는 것만 제외하면-한 것이다. 최소 제곱 오차가 아닌 발산값을 비용 함수로 고려하는 경우에 이 행렬 분해는, 이미 대중적인 문서 군집 방법인 확률적 잠재 의미 분석과 동일하다.

다른 학습기법과의 관계

• Learning the parts of objects by non-negative matrix factorization에서는 음수 미포함 행렬 분해를 이용하여 부분 기반 사진 분해를 하였다. 이 논문에서 음수 미포함 행렬 분해를 벡터 정량화나 주성분 분석 기법과 비교했는데, 세 기법 모두 분해를 기반하고 있지만 제약 조건이 달라 결과가 모두 다르게 나왔다.

• 음수 미포함 행렬 분해는 좀 더 일반적인 확률 모델인 다항 주성분 분석 기법과 동일시 될 수 있다. 특히, Kullback-Leibler 발산값을 최소화시키면, 음수 미포함 행렬 분해는 확률적 잠재 의미 분석과 동일시 될 수 있다.

• 음수 미포함 행렬 분해는 완화된 형태의 k 평균 알고리즘으로 동일시 할 수 있다. 이는 음수 미포함 행렬 분해를 데이터 군집화에 사용하는 이론적 토대가 된다. 그러나 k-평균 알고리즘은 음수 미포함이라는 제약 조건을 가지고 있지 않다는 차이가 있다.

• 음수 미포함 행렬 분해는 2개 층을 가진 베이즈 네트워크 모델로 볼 수도 있다.

응용 사례

텍스트 마이닝

음수 미포함 행렬 분해는 텍스트 마이닝에 응용할 수 있다. 텍스트 마이닝에서 문서-용어 행렬은 문서에서 용어들의 가중치 정보를 담고 있다. 이 행렬은 음수 미포함 행렬 분해를 이용하여 용어-요소 행렬과 요소-문서 행렬로 분해할 수 있다. 이 요소들은 문서의 내용으로부터 도출되고, 요소-문서 행렬은 관련 문서들의 정보 군집에 대한 정보를 담는다.

스펙트럼 데이터 분석

음수 미포함 행렬 분해는 스펙트럼 데이터 분석에 응용할 수 있다. 한 가지 예시로, 음수 미포함 행렬은 우주 상의 물체와 파편을 구분짓는데 쓰였다.

생물 정보 공학

음수 미포함 행렬 분해는 유전자 발현 데이터를 그룹화하고, 군집된 데이터의 대표적인 유전자를 찾는데에 응용할 수 있다.

인터넷 거리 예측

음수 미포함 행렬 분해는 인터넷 상의 거리 예측에 응용할 수 있다. 예를 들어, N개의 호스트가 있다고 하자. 각각의 호스트 사이의 거리 정보는 N×N 행렬 안에 담을 수 있고, 이를 예측해 볼 수 있다.

최근 연구 동향

음수 미포함 행렬 분해에서는 다양하게 연구가 진행되고 있지만, 특히 다음 영역에서의 연구를 포함한다.

알고리즘

요소의 초기화나 요소의 광역 최소값을 찾는 법에 대한 연구가 진행 중이다.

확장성

엄청나게 큰 크기의 행렬을 분해하는 방법에 대한 연구가 진행 중이다. 웹 데이터 마이닝 분야 같은 곳에서는 굉장히 큰 데이터가 빈번하게 쓰여 지고 있고, 이는 분산 기법을 도입한 분산 음수 미포함 행렬 분해에 대한 연구로 이어지고 있다.

동적 학습

데이터가 들어올 때마다 분해를 업데이트 해줄 수 있는 연구가 진행 중이다.

관련 라이브러리

C

Linux에서 이용할 수 있다. http://www.cs.virginia.edu/~jdl/nmf/

Python

파이썬은 자체적으로 nimfa라는 NMF 라이브러리를 가지고 있다. 관련 API: http://nimfa.biolab.si/

JAVA

자바에서 기계학습을 위한 라이브러리를 제공하는 곳이다. http://sourceforge.net/projects/jlml/files/JML/

Matlab

매트랩에는 음수 미포함 행렬 분해를 수행하는 함수가 있다. 관련 API: http://kr.mathworks.com/help/stats/nnmf.html

참조 논문 및 자료

Others

• J. Shen, G. W. Israël (1989). “A receptor model using a specific non-negative transformation technique for ambient aerosol”. 《Atmospheric Environment》 23 (10): 2289–2298. doi:10.1016/0004-6981(89)90190-X. 
• Pentti Paatero (1997). “Least squares formulation of robust non-negative factor analysis”. 《Chemometrics and Intelligent Laboratory Systems》 37 (1): 23–35. doi:10.1016/S0169-7439(96)00044-5. 
• Raul Kompass (2007). “A Generalized Divergence Measure for Nonnegative Matrix Factorization”. 《Neural Computation》 19 (3): 780–791. doi:10.1162/neco.2007.19.3.780. PMID 17298233. 
• Liu, W.X. and Zheng, N.N. and You, Q.B. (2006). “Nonnegative Matrix Factorization and its applications in pattern recognition” (PDF). 《Chinese Science Bulletin》 51 (17–18): 7–18. doi:10.1007/s11434-005-1109-6.  CS1 관리 - 여러 이름 (링크)
• Ngoc-Diep Ho, Paul Van Dooren and Vincent Blondel (2008). “Descent Methods for Nonnegative Matrix Factorization”. arXiv:0801.3199 [cs.NA]. 
• Andrzej Cichocki, Rafal Zdunek and Shun-ichi Amari (2008). “Nonnegative Matrix and Tensor Factorization”. 《IEEE Signal Processing Magazine》 25 (1): 142–145. doi:10.1109/MSP.2008.4408452. 
• Cédric Févotte, Nancy Bertin, and Jean-Louis Durrieu (2009). “Nonnegative Matrix Factorization with the Itakura-Saito Divergence: With Application to Music Analysis”. 《Neural Computation》 21 (3): 793–830. doi:10.1162/neco.2008.04-08-771. PMID 18785855.  CS1 관리 - 여러 이름 (링크)
• Ali Taylan Cemgil (2009). “Bayesian Inference for Nonnegative Matrix Factorisation Models”. 《Computational Intelligence and Neuroscience》 2009 (2): 1. doi:10.1155/2009/785152. PMC 2688815. PMID 19536273.