복소해석학에서, 코시 적분 정리(-積分定理, 영어: Cauchy's integral theorem)는 단일 연결 열린집합 위의 정칙 함수의 경로 적분이 경로와 무관하다는 정리이다.
정의
유계 연결 열린집합  의 경계
의 경계  가 유한 개의 조각마다
가 유한 개의 조각마다  곡선으로 이루어졌고, 양의 방향을 가지며, 연속 함수
곡선으로 이루어졌고, 양의 방향을 가지며, 연속 함수  가
가  에서 정칙 함수라고 하자. 코시 적분 정리에 따르면, 다음이 성립한다.[1]:84
에서 정칙 함수라고 하자. 코시 적분 정리에 따르면, 다음이 성립한다.[1]:84

이에 따라, 단일 연결 열린집합  위의 정칙 함수
위의 정칙 함수  의, 임의의 두 점
의, 임의의 두 점  사이의 경로 적분
사이의 경로 적분

는 경로
![{\displaystyle \gamma \colon [a,b]\to D\qquad (\gamma (a)=z',\;\gamma (b)=z'')}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e0430dbd62f9ff26ec9af8ad7a5c8802cda12c2)
의 선택에 의존하지 않는다.
증명
C1을 가정하는 증명
도함수  가
가  의 어떤 근방
의 어떤 근방  에서 연속 함수임을 가정할 경우,[1]:84-85
에서 연속 함수임을 가정할 경우,[1]:84-85

인  를 취하자. 그렇다면, 그린 정리와 코시-리만 방정식에 의하여,
를 취하자. 그렇다면, 그린 정리와 코시-리만 방정식에 의하여,

이다.
C1을 가정하지 않는 증명
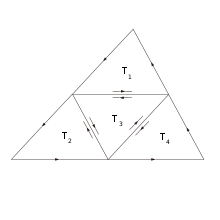 삼각형 열린집합에 대한 코시 적분 정리의 증명 도해
삼각형 열린집합에 대한 코시 적분 정리의 증명 도해
위와 같은 가정을 사용하지 않을 경우, 우선  가 삼각형 열린집합인 경우를 보이자.[1]:85-87
가 삼각형 열린집합인 경우를 보이자.[1]:85-87
귀류법을 사용하여,

이라고 가정하자.  라고 하고, 삼각형 열린집합
라고 하고, 삼각형 열린집합  의 세 변의 중점을 이어 얻는 4개의 작은 삼각형 열린집합
의 세 변의 중점을 이어 얻는 4개의 작은 삼각형 열린집합  를 생각하자. 그렇다면,
를 생각하자. 그렇다면,

이므로,

인  가 존재한다. 이와 같이 반복하면, 다음을 만족시키는 삼각형 열린집합의 열
가 존재한다. 이와 같이 반복하면, 다음을 만족시키는 삼각형 열린집합의 열  을 얻는다.
을 얻는다.




따라서,

인  가 존재하며, 임의의
가 존재하며, 임의의  에 대하여,
에 대하여,

이다.

이므로, 이는 모순이다.
이제, 일반적인 경우를 보이자.  는 유한 개의 단일 연결 열린집합의 합집합으로 분할되므로, 편의상
는 유한 개의 단일 연결 열린집합의 합집합으로 분할되므로, 편의상  가 단일 연결 열린집합이라고 가정하자.
가 단일 연결 열린집합이라고 가정하자.
임의의  에 대하여,
에 대하여,  는 균등 연속 함수이므로, 다음을 만족시키는 다각형 열린집합
는 균등 연속 함수이므로, 다음을 만족시키는 다각형 열린집합  가 존재한다.
가 존재한다.


다각형 열린집합  는 유한 개의 삼각형 열린집합의 합집합으로 분할되므로,
는 유한 개의 삼각형 열린집합의 합집합으로 분할되므로,

이며, 따라서

이다.
각주
외부 링크
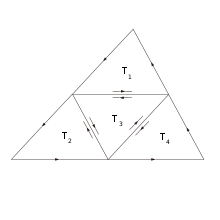










![{\displaystyle \gamma \colon [a,b]\to D\qquad (\gamma (a)=z',\;\gamma (b)=z'')}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e0430dbd62f9ff26ec9af8ad7a5c8802cda12c2)





























