투수계수는 다르시의 법칙에 사용되는 계수로, 유체가 얼마나 잘 다공성 매질을 통과하는지 나타낸다.
투수계수에 영향을 주는 인자[편집]
매질과 통과 유체에 따라 투수계수가 결정된다. 매질의 경우 유효입경 D10, 공극비 e,[주 1] 비표면적 S 등을 인자로 가지고, 유체의 경우 단위중량 γ, 점성계수 η 등을 인자로 가진다. 다음은 투수계수를 결정하는 몇 가지 식이다.
Hazen의 경험식(1930)
 , 균등계수
, 균등계수  인 균등한 가는 모래의 경우 다음 경험식을 적용할 수 있다. c가 1.0에서 1.5 사이의 상수라고 할 때,
인 균등한 가는 모래의 경우 다음 경험식을 적용할 수 있다. c가 1.0에서 1.5 사이의 상수라고 할 때,

Taylor의 식(1948)
C가 형상계수라고 할 때,[2]

- Ds : 토립자 입경(cm)
Kozeny-Carman 식
Taylor의 식을 수정한 식이다. k0는 공극의 형상과 두 점 사이의 거리에 대한 실제 흐름 길이에 따른 계수이다.

Lambe-Whitman 식

일반적으로 m/day를 쓰지만 빠르게 이동하는 물에 대해서는 cm/hr를 쓰기도 한다.
실내시험으로는 투수계수를 정수위 투수시험과 변수위 투수시험으로 결정할 수 있다. 현장시험으로는 양수시험, 피압 지하수 우물(artesian well) 양수법, 시추공을 이용하는 방법(개단시험, 패커시험)이 있다.
실내시험[편집]
정수위 투수시험[편집]
 정수위 투수시험
정수위 투수시험
투수성이 비교적 큰 조립토에 적당하다. 흙 시료에 유입되는 수조와 유출되어 나오는 수조의 수위를 일정하게 하여 물을 시료에 통과시킴으로써 다르시의 법칙에 의해 투수계수를 구할 수 있다. 시험기구는 정압수두 투수계라고 부른다.


- Q : 침투수량
- A : 시료 단면적
- t : 투수 시간
- L : 시료 길이
변수위 투수시험[편집]
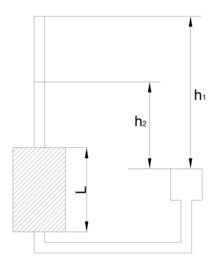 변수위 투수시험. 시간이 t1일 때 수위가 h1이다가 t2가 되면 h2로 변한다.
변수위 투수시험. 시간이 t1일 때 수위가 h1이다가 t2가 되면 h2로 변한다.
투수성이 비교적 작은 세립토에 적당하다. 정수위 시험과는 다르게 유입수가 스탠드파이프를 통해 흙 시료를 빠져나간다. 따라서 수위가 변한다. 파이프 단면적을 a, 시료 단면적을 A라 할 때 투수계수는 다음과 같다. 시험기구는 감소수두 투수계라고 한다.

이 식은 다르시의 법칙과 연속방정식을 적분하여 나온 것이다.

다르시의 법칙에 의해
 이므로
이므로

적분하면


이것을 k에 대해 정리하면 변수위 투수시험의 투수계수가 나온다.
온도 보정[편집]
정수위 투수시험, 변수위 투수시험을 통해 구한 투수계수를 15°C에서의 투수계수로 바꾸어주어야 한다. 온도가 T°C일 때의 투수계수를 kT, 점성계수를 μT, 온도가 15°C일 때의 투수계수를 k15, 점성계수를 μ15라고 하면 다음 식으로 보정할 수 있다.

현장시험[편집]
현장시험은 실내시험에 비해 교란되지 않은 시료를 이용할 수 있으므로 신뢰성이 높다는 장점이 있다.
양수시험[편집]
 하나의 시험정을 파고 주위에 여러 개의 관측정을 파서 투수계수를 측정하는 양수시험
하나의 시험정을 파고 주위에 여러 개의 관측정을 파서 투수계수를 측정하는 양수시험
하나의 시험정과 여러 개의 관측정을 파고, 시험정에서 일정량의 물을 양수하면서 관측정의 수위를 측정하여 투수계수를 정하는 것을 양수시험이라고 한다. 양수시험을 통해 구하는 투수계수는 다음과 같다. 양수량을 Q라고 할 때,

만약 시험정 근처에 관측정을 파고, 원래 양수 전 지하수위에 또다른 관측정이 있다면  이므로 식은 다음과 같이 된다.
이므로 식은 다음과 같이 된다.

피압 지하수 우물 양수법[편집]
불투수층 사이에 피압 지하수층(confined aquifer)이 T의 두께만큼 존재하는 경우에도 양수시험을 하여 투수계수를 구할 수 있다.

성층토층 평균투수계수[편집]
토층이 다양한 경우 투수계수는 각 토층의 불교란 시료를 채취하여 각각의 투수계수를 측정한 후 전체 토층의 평균투수계수를 구하는 방법을 쓴다.
수평토층 평균투수계수[편집]
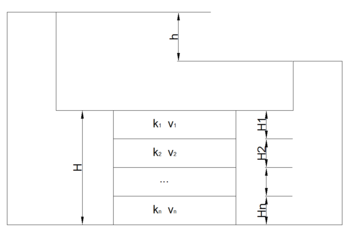
각 토층의 단위폭당 유량( )을 전부 합하면 전체 토층의 평균투수계수를 이용한 단위폭당 유량(q)과 같다는 원리를 이용한다.
)을 전부 합하면 전체 토층의 평균투수계수를 이용한 단위폭당 유량(q)과 같다는 원리를 이용한다.



수직토층 평균투수계수[편집]

각 토층을 지나면서 생기는 수두손실을  이라고 하자. 모든 토층을 지났을 때 수두손실
이라고 하자. 모든 토층을 지났을 때 수두손실  이며, 이것을 각 토층의 동수경사와 토층 두께로 나타낸다면 다음과 같이 된다.
이며, 이것을 각 토층의 동수경사와 토층 두께로 나타낸다면 다음과 같이 된다.

토층을 지나는 유량이 모두 동일하기 때문에  이며, 연속방정식에 의하면 유속도 모두 동일하다(
이며, 연속방정식에 의하면 유속도 모두 동일하다( ) 이를 각 토층의 투수계수와 동수경사로 나타낸다.
) 이를 각 토층의 투수계수와 동수경사로 나타낸다.

전체 토층에서 유속으로부터



등가투수계수[편집]
자연계 토질은 대부분 비등방성이다. 연직방향 투수계수가 수평방향 투수계수보다 작다( ) 연속방정식을 라플라스 방정식으로 바꾸면 x방향으로 축소된 유선망을 그릴 수 있다. 즉 축소된 좌표는 다음과 같이 변환된다.
) 연속방정식을 라플라스 방정식으로 바꾸면 x방향으로 축소된 유선망을 그릴 수 있다. 즉 축소된 좌표는 다음과 같이 변환된다.

침투가 x방향으로만 일어난다고 할 때, 단위폭당 침투유량은

 은 등가투수계수이다.
은 등가투수계수이다.
같이 보기[편집]
내용주[편집]
- ↑ 토양 내 공기가 들어가면 투수계수가 감소한다.
참조주[편집]
- ↑ 임진근 외 (2015). 《토목기사 과년도 - 토질 및 기초》. 성안당. 4-6쪽.
참고 문헌[편집]









































