채우기 문제
채우기 문제(영어: packing problems)는 물체를 용기에 채우는 수학의 최적화 문제이다. 목표는 하나의 용기에 물체를 가능한 한 빽빽하게 채우거나 모든 물체를 가능한 한 적은 용기에 채우는 것이다. 이 문제의 대부분은 실생활에 포장, 저장 그리고 수송 문제와 관계지을 수 있다. 각 채우기 문제는 이중 덮기 문제가 있다. 이것은 겹치는 것을 허용하여 용기의 모든 영역을 동일한 물체로 완전히 덮는데 몇 개가 들어가는지를 구하는 문제이다.
상자 채우기 문제는 다음이 주어진다:
- '용기' (보통 단일 2 또는 3차원 볼록한 영역이나 무한한 공간이다)
- 일부 또는 모두가 하나 이상의 용기에 들어가야 하는 '물체'의 집합. 집합은 크기가 정해진 다른 물체 또는 반복해서 사용할 수 있는 유일한 고정된 차원의 물체를 포함한다.
보통 채우기는 물건과 다른 물건 사이나 용기 벽 사이에 겹치는 일이 없어야 한다. 일부 변형에서 초점은 용기에 최대 밀도로 채우는 구성을 찾는 것이다. 더 일반적으로 목표는 가능한 적은 용기에 모든 물체를 담는 것이다.[1] 어떤 변형에서 (물체와 물체간 그리고/또는 용기의 경계에서) 겹치는 것은 허락되지만 최소화되어야 한다.
무한 공간 채우기[편집]
이 문제의 대부분에서 용기의 크기가 모든 방향으로 커질 때 무한 유클리드 공간을 최대한 빽빽하게 채우는 문제와 같아진다. 이 문제는 많은 과학 분야와 관련이 있으며 중대한 관심을 받고 있다. 케플러의 추측은 구 채우기의 최적해를 몇백년 전에 제시되었고, 토머스 캘리스터 헤일즈(Thomas Callister Hales)가 증명했다. 타원체[2], 사면체[3][4]를 포함한 플라톤과 아르키메데스 다면체와 불평등 구형 이합체[5]와 같은 많은 모양들도 관심을 받았다.
육각형 원 채우기[편집]

이 문제는 수학적으로 원 채우기 정리의 아이디어와는 다르다. 관련된 원 채우기 문제는 평면이나 구의 표면에서 원의 크기가 다를 수 있는 원을 채우는 것을 다룬다.
다른 차원의 구는 일차원 보다 큰 차원에서 완벽히 효율적으로 채울 수 없다(일차원 우주에서, 원과 비슷한 것은 단지 두 점 뿐이다). 다시 말해, 원으로만 채울 때는 항상 사용하지 않은 공간이 있다. 원을 가장 효율적으로 채우는 방법인 육각형 채우기는 대략적으로 91%의 효율을 얻을 수 있다.[6]
높은 차원에서 구 채우기[편집]
3차원에서 면심입방구조는 가장 좋은 격자 채우기이기 때문에 최적의 채우기라고 여겨진다. 3차원에서 '단순'한 구 채우기('단순' 은 조심스럽게 정의해야 한다)는 정의 가능한 9가지가 있다.[7] 8차원 E8 격자와 24차원 리치 격자는 각각 실 차원 공간에서 최적으로 증명되었다.
3차원에서 정다면체 채우기[편집]
정육면체는 3차원 공간을 완전히 채우도록 배열할 수 있다, 가장 자연스러운 채우기는 정육면체 벌집이다. 다른 정다면체는 공간을 스스로 채울 수 없지만 몇 가지 예비 결과가 알려져 있다. 정사면체는 적어도 85%의 채우기를 할 수 있다. 정십이면체의 최대 채우기는 앞에서 말한 면심 입방 격자(FCC)를 기반으로 한다.
정사면체와 정팔면체는 정사면체-정팔면체 벌집으로 알려진 배열로 공간을 채울 수 있다.
| 물체 | 격자 채우기의 최적 밀도 |
|---|---|
| 정이십면체 | 0.836357...[8] |
| 정십이면체 | (5 + √5)/8 = 0.904508...[8] |
| 정팔면체 | 18/19 = 0.947368...[9] |
국소 발전 방법과 무작위 채우기를 결합한 시뮬레이션은 정이십면체, 정십이면체, 정팔면체에 대한 격자 채우기가 모든 채우기에서 최적이라는 것을 나타낸다.[10]
3차원 용기에 채우기[편집]
입방체에 입방체[편집]
주어진 입방체(3차원 직사각형)의 집합으로 채울 수 있는 최소 입방체 용기의 개수를 결정한다. 채우려는 육면체는 각 축을 기준으로 90도 회전시킬 수 있다.
유클리드 공에 구[편집]
개의 분리된 열린 단위 공으로 채울 수 있는 가장 작은 공을 찾는 문제는 이고 제한 없는 무한 차원의 힐베르트 공간에 있을 때, 차원 유클리드 공간에서 간단하고 완벽한 답이 있다. 일반적인 문제의 취지를 밝히기 위해 자세히 설명할 필요가 있다. 이 경우에 쌍의 접하는 단위 공의 조합이 가능하다. 중심을 모서리가 2개인 차원 단체의 꼭짓점 에 두자; 이것은 쉽게 정규직교 기반에서 시작하는 것을 알 수 있다. 조금 계산해 보면, 무게중심에서 꼭짓점 까지의 거리는 이라는 것을 알 수 있다. 게다가, 공간의 다른 모든 점은 필연적으로 개의 정점 중 적어도 하나로부터 더 큰 거리를 갖는다. 공의 포함관계를 생각하면, 를 중심으로 하는 개의 열린 단위 공은 이 조합에서 최소의 반경 을 갖는 원에 들어있다.
이 조합이 최적임을 보이기 위해서, 중심이 이고 반지름이 인 원 안에 있는 개의 분리된 열린 단위 공의 중심을 이라고 하자. 유한집합 에서 로 대응시키자. 모든 에 대해서 를 로 대응시키자. 모든 에 대해서 일 때 이 대응은 1-Lipschitz 이고, Kirszbraun 정리에 의해서 이는 전역적으로 정의된 1-Lipschitz 매핑으로 확장된다; 특히, 모든 에 대해서 이기 때문에 또한 인 점이 존재한다. 이것은 오직 일 때 만 개의 분리된 열린 단위 공들이 반지름이 인 공 안에 있을 수 있다는 것을 보여준다. 무한차원 힐베르트 공간에서 이것은 . 예를 들어, 를 중심으로 가지고 은 정규 직교 기반인 단위 공은 원점을 중심으로 하고 반지름이 인 원에 분리되어서 포함되어있다. 게다가 일 때는 반지름이 인 공 안에 들어갈 수 있는 분리된 열린 단위 공의 최대 개수는 .
입방체에 구[편집]
a × b × c.의 크기를 가지는 직육면체에 지름 d인 구체가 몇 개가 들어갈 지를 결정한다.
원기둥에 구[편집]
반지름이 R 이고 반지름이 r (< R)인 n개의 구가 들어갈 원기둥의 높이 h를 결정한다.[11]
2차원 용기에 채우기[편집]
원 채우기[편집]
원에 원[편집]

단위원 n개로 가장 작은 원을 채운다. 이것은 단위원에 점을 퍼뜨려 가장 큰 첨들간 최소거리 dn를 찾는 문제와 매우 유사한 문제이다.
n ≤ 13일 때와 n = 19일 때 최적해가 증명되었다.
정사각형에 원[편집]

단위원 n개로 가장 작은 정사각형을 채운다. 이것은 단위원에 점을 퍼뜨려 가장 큰 점들간 최소거리 dn를 찾는 문제와 매우 유사한 문제이다.[12] 이 두 문제를 변환하려면 단위 원이 있는 정사각형의 한 변의 길이는 L = 2 + 2/dn이다.
n ≤ 30일 때 최적해가 증명되었다.[13]
직각이등변삼각형에 원[편집]

단위원 n개로 가장 작은 직각이등변삼각형에 채운다. n<300일 때 좋은 근사가 알려져 있다.[14]
정삼각형에 원[편집]
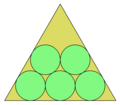
단위원 n개로 가장 작은 정삼각형을 채운다. n<13일 때 최적해가 알려져 있고, n < 28일 때 추측 가능하다.[15]
정사각형 채우기[편집]
정사각형에 정사각형[편집]

단위 정사각형 n개를 가능한 작은 정사각형에 넣는다.
최적해는 n = 1–10, 14–16, 22–25, 33–36, 62–64, 79–81, 98–100, 그리고 모든 사각수일 때 증명되었다.[16][17]
낭비되는 공간은 점근적으로 O(a7/11)이다.[18]
원에 정사각형 채우기[편집]
정사각형 n개를 가능한 작은 원에 넣는다.
최소해:[19]
| 정사각형의 개수 | 원의 반지름 |
|---|---|
| 1 | 0.707... |
| 2 | 1.118... |
| 3 | 1.288... |
| 4 | 1.414... |
| 5 | 1.581... |
| 6 | 1.688... |
| 7 | 1.802... |
| 8 | 1.978... |
| 9 | 2.077... |
| 10 | 2.121... |
| 11 | 2.214... |
| 12 | 2.236... |
직사각형 채우기[편집]
직사각형에 크기가 동일한 직사각형[편집]
크기가 (l,w)인 직사각형 여러개를 90° 회전을 허용하여 크기가 (L,W)인 큰 직사각형 안에 채우는 문제는 파렛트에 상자를 싣거나 특히 나무 펄프 보관 등의 적용이 있다.
예를 들어, 크기가 (137,95)인 직사각형 147개는 크기가 (1600,1230)인 직사각형을 채울 수 있다.[20]
직사각형에 크기가 다른 직사각형[편집]
다양한 너비와 높이를 가지는 직사각형들을 최소 면적의 (하지만 둘러싸는 직사각형의 너비와 높이에는 경계가 없는) 직사각형에 채우는 문제는 이미지들을 하나의 큰 이미지로 결합할 때 중요한 문제이다. 각각의 이미지를 웹 서버에 요청하기 때문에, 하나의 큰 이미지를 로딩하는 웹 페이지는 같은 페이지에서 여러 작은 이미지를 로딩하는 브라우저보다 빠르다.
다양한 너비와 높이를 가지는 직사각형들을 최소넓이의 직사각형에 채우는 빠른 알고리즘의 예는 여기 있다.
관련 분야[편집]
타일링이나 테셀레이션 문제에서 틈이나 겹치는 것이 없어야한다. 이런 종류의 퍼즐의 대부분은 직사각형이나 폴리오미노를 큰 직사각형이나 사각형같은 모양에 채우는 문제와 관련되어있다.
직사각형(과 직육면체)를 직사각형 (직육면체)에 틈이나 겹침없는 타일링에 대해서는 상당히 많은 정리들이 있다:
- 오직 a가 n으로 나눠지거나 b가 n으로 나눠질 때만 a × b 의 직사각형은 1 × n의 띠로 채워진다.[21][22]
- 드 브루인의 정리: 상자가 어떤 자연수 p, q, r에 대해 a p × a b q × a b c r 일 때(즉, 상자가 벽돌의 배 일 때) a × a b × a b c 의 조화 벽돌로 상자를 채울 수 있다.
폴리오미노 타일링 연구는 크게 두 종류의 문제로 나뉜다: 합동인 타일로 직사각형을 타일링 하고, 각 폴리오미노를 직사각형에 채운다.
두번째 종류의 고전 퍼즐은 펜토미노 12개 전부를 크기가 3×20, 4×15, 5×12 또는 6×10인 직사각형에 배열하는 것이다.
불규칙한 물체 채우기[편집]
불규칙한 물체 채우기는 폐쇄적인 해결법에는 적합하지 않다; 하지만 실용 환경 과학에 적용은 매우 중요하다. 예를 들어, 불규칙한 모양의 흙 입자를 크기와 모양을 다양하게 채우기는 식물종의 뿌리 형성과 토양에서 물의 움직임에 중요하다.[23]
같이 보기[편집]
- 집합 채우기
- 상자 채우기 문제
- Slothouber–Graatsma 퍼즐
- 콘웨이 퍼즐
- 테트리스
- 덮기 문제
- 배낭 문제
- 정사면체 채우기
- 원료 절단 문제
- 입맞춤 수 문제
- 구 채우기
- 무작위 채우기
각주[편집]
- ↑ Lodi, A., Martello, S., Monaci, M. (2002). “Two-dimensional packing problems: A survey”. 《European Journal of Operational Research》 (Elsevier) 141: 241–252. doi:10.1016/s0377-2217(02)00123-6.
- ↑ Donev, A.; Stillinger, F.; Chaikin, P.; Torquato, S. (2004). “Unusually Dense Crystal Packings of Ellipsoids”. 《Physical Review Letters》 92 (25): 255506. arXiv:cond-mat/0403286. Bibcode:2004PhRvL..92y5506D. doi:10.1103/PhysRevLett.92.255506. PMID 15245027.
- ↑ Haji-Akbari, A.; Engel, M.; Keys, A. S.; Zheng, X.; Petschek, R. G.; Palffy-Muhoray, P.; Glotzer, S. C. (2009). “Disordered, quasicrystalline and crystalline phases of densely packed tetrahedra”. 《Nature》 462 (7274): 773–777. arXiv:1012.5138. Bibcode:2009Natur.462..773H. doi:10.1038/nature08641. PMID 20010683.
- ↑ Chen, E. R.; Engel, M.; Glotzer, S. C. (2010). “Dense Crystalline Dimer Packings of Regular Tetrahedra”. 《Discrete & Computational Geometry》 44 (2): 253–280. doi:10.1007/s00454-010-9273-0.
- ↑ Hudson, T. S.; Harrowell, P. (2011). “Structural searches using isopointal sets as generators: Densest packings for binary hard sphere mixtures”. 《Journal of Physics: Condensed Matter》 23 (19): 194103. doi:10.1088/0953-8984/23/19/194103.
- ↑ http://mathworld.wolfram.com/CirclePacking.html
- ↑ Smalley, I.J. 1963. Simple regular sphere packings in three dimensions. Mathematics Magazine 36, 295-299. doi:10.2307/2688954
- ↑ 가 나 Betke, U. & Henk, M. Densest lattice packings of 3-polytopes. Comput. Geom. 16, 157–186 (2000)
- ↑ Minkowski, H. Dichteste gitterfo¨rmige Lagerung kongruenter Ko¨rper. Nachr. Akad. Wiss. Go¨ttingen Math. Phys. KI. II 311–355 (1904).
- ↑ Torquato, S.; Jiao, Y. (Aug 2009). “Dense packings of the Platonic and Archimedean solids”. 《Nature》 460 (7257): 876–879. arXiv:0908.4107. Bibcode:2009Natur.460..876T. doi:10.1038/nature08239. ISSN 0028-0836. PMID 19675649.
- ↑ Stoyan, Y. G.; Yaskov, G. N. (2010). “Packing identical spheres into a cylinder”. 《International Transactions in Operational Research》 17: 51–70. doi:10.1111/j.1475-3995.2009.00733.x.
- ↑ Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K. (1991). 《Unsolved Problems in Geometry》. New York: Springer-Verlag. 108–110쪽. ISBN 0-387-97506-3.
- ↑ Eckard Specht (2010년 5월 20일). “The best known packings of equal circles in a square”. 2010년 5월 25일에 확인함.
- ↑ Specht, Eckard (2011년 3월 11일). “The best known packings of equal circles in an isosceles right triangle”. 2011년 5월 1일에 확인함.
- ↑ Melissen, J. (1995). “Packing 16, 17 or 18 circles in an equilateral triangle”. 《Discrete Mathematics》 145: 333–342. doi:10.1016/0012-365X(95)90139-C.
- ↑ Erich Friedman, "Packing unit squares in squares: a survey and new results" Archived 2009년 7월 27일 - 웨이백 머신, The Electronic Journal of Combinatorics DS7 (2005).
- ↑ Wolfram Bentz (2016년 6월 12일). “Optimal Packings of 22 and 33 Unit Squares in a Square”. arXiv:1606.03746.
- ↑ Erdős, P.; Graham, R. L. (1975). “On packing squares with equal squares” (PDF). 《Journal of Combinatorial Theory, Series A》 19: 119–123. doi:10.1016/0097-3165(75)90099-0.
- ↑ “보관된 사본”. 2017년 9월 14일에 원본 문서에서 보존된 문서. 2017년 9월 14일에 확인함.
- ↑ Birgin, E G; Lobato, R D; Morabito, R (2010). “An effective recursive partitioning approach for the packing of identical rectangles in a rectangle”. 《Journal of the Operational Research Society》 61: 306–320. doi:10.1057/jors.2008.141.
- ↑ Honsberger, Ross (1976). 《Mathematical Gems II》. The Mathematical Association of America. 67쪽. ISBN 0-88385-302-7.
- ↑ Klarner, D.A.; Hautus, M.L.J (1971). “Uniformly coloured stained glass windows”. 《Proceedings of the London Mathematical Society》. 3 23: 613–628. doi:10.1112/plms/s3-23.4.613.
- ↑ C.Michael Hogan. 2010. Abiotic factor. Encyclopedia of Earth. eds Emily Monosson and C. Cleveland. National Council for Science and the Environment. Washington DC
외부 링크[편집]
- Optimizing Three-Dimensional Bin Packing Archived 2019년 3월 3일 - 웨이백 머신
- API for 3D bin packing
- 3D Boxes and Cylinders packing with telescoping
수학 잡지같이 많은 퍼즐 책은 채우기 문제를 포함하고 있다.
- Links to various MathWorld articles on packing
- MathWorld notes on packing squares.
- Erich's Packing Center Archived 2010년 3월 14일 - 웨이백 머신
- www.packomania.com 표, 그래프, 계산기, 참조 등이 있는 사이트이다.
- "Box Packing" by Ed Pegg, Jr., the Wolfram Demonstrations Project, 2007.
- Best known packings of equal circles in a circle, up to 1100
- Circle packing challenge problem in Python






























