읽고 말하기 수열

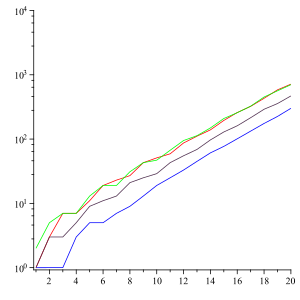
이 선들은 23 (빨강), 1 (파랑), 13 (보라), 312 (초록)으로 시작하는 읽고 말하기 수열의 자릿수를 나타낸다. 이 선은 (로그 수직 척도로 나타냈을 때) 기울기가 콘웨이 상수인 직선으로 접근한다.

읽고 말하기 수열은 다음과 같이 시작하는 수열이다. 대한민국에서는 소설인 개미에서 소개되면서 유명해졌기 때문에, 개미 수열이란 이름으로 잘 알려져 있다.

1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, ... (OEIS의 수열 A005150)

이 수열은 앞의 수를 연속된 같은 수의 개수로 묶어서 읽는 방식으로 만들어진다..

• 1을 "1개의 1"로 읽는다: 11
• 11을 "2개의 1"로 읽는다: 21
• 21을 "1개의 2와, 1개의 1"로 읽는다: 1211
• 1211을 "1개의 1과, 1개의 2와, 2개의 1"로 읽는다: 111221
• 111221을 "3개의 1과, 2개의 2와, 1개의 1"로 읽는다: 312211
• 312211을 "1개의 3과, 1개의 1과, 2개의 2와, 2개의 1"로 읽는다: 13112221

반복 길이 부호화 알고리즘에서 이와 비슷한 원리를 이용한다.

공식

$a(n+1)=A045918(a(n))$ 여기서 A045918는 OEIS 수열

또는

$a(n)=\sum _{k=1}^{A005341(n)}A03402(n,k)\cdot 10^{A005341(n)-k}$ 여기서 A005341및 A03402는 OEIS 수열

성질

• 수열은 무한히 길어진다. 초기값을 1이 아닌 다른 정수로 시작해서 똑같은 알고리즘을 적용하여 만들어도 마찬가지로 무한하게 길어진다. 단 한가지 예외는 22로 시작한 수열이다. 이 수열은 22, 22, 22, ...로 길이가 더이상 늘어나지 않는다.
• 수열에서 1, 2, 3이 아닌 수는 등장하지 않는다. 이 성질은 초기값 자체에 그 외의 숫자가 들어가거나, 초기값에 연속으로 3개를 초과하는 똑같은 숫자가 들어가지 않는 이상 유효하다.
• $L_{i}$를 수열의 $i$번째 수열의 길이라고 하면,

$\lim _{i\to \infty }{\frac {L_{i+1}}{L_{i}}}=\lambda$

여기서 $\lambda =1.303577269\ldots$ 차수가 71인 대수적 수로 콘웨이 상수라고 부른다. 존 호턴 콘웨이가 이것을 증명했으며, 초기값이 22가 아닌 수열에 대해 같은 값으로 수렴한다.

콘웨이 상수는 다음 다항식의 유일한 양의 실수해이다.

$x^{71}-x^{69}-2x^{68}-x^{67}+2x^{66}+2x^{65}+x^{64}-x^{63}-x^{62}-x^{61}-x^{60}-x^{59}+$

$2x^{58}+5x^{57}+3x^{56}-2x^{55}-10x^{54}-3x^{53}-2x^{52}+6x^{51}+6x^{50}+x^{49}+9x^{48}-3x^{47}-$

$7x^{46}-8x^{45}-8x^{44}+10x^{43}+6x^{42}+8x^{41}-5x^{40}-12x^{39}+7x^{38}-7x^{37}+7x^{36}+x^{35}-$

$3x^{34}+10x^{33}+x^{32}-6x^{31}-2x^{30}-10x^{29}-3x^{28}+2x^{27}+9x^{26}-3x^{25}+14x^{24}-8x^{23}-$

$7x^{21}+9x^{20}+3x^{19}-4x^{18}-10x^{17}-7x^{16}+12x^{15}+7x^{14}+2x^{13}-12x^{12}-4x^{11}-$

$2x^{10}+5x^{9}+x^{7}-7x^{6}+7x^{5}-4x^{4}+12x^{3}-6x^{2}+3x-6=0$

같이 보기

• 콜라코스키 수열(Kolakoski sequence)
• 오토그램(Autogram)
• 깃스윗츠 수열(Gijswijt sequence)

각주

• 매스월드