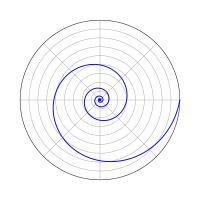
로그 나선
로그 나선(Logarithmic spiral), 대수 나선(형), 등각 나선형 또는 성장 나선형은 종종 자연에 나타나는 나선형 곡선을 표현하는데 유용하다.
로그 나선형은 데카르트에 의해 처음 기술되었으며, 나중에는 야콥 베르누이가 "스피라 미라빌리스(Spira mirabilis)"로 불리는 놀라운 나선형 (the marvelous spiral)현상을 광범위하게 조사했다.[1]
정의[편집]
극좌표에서 () 로그 나선형 곡선은 다음과 같이 표현할 수 있다.[2]
또는,
- 자연 대수의 기초가 되는 그리고 와 는 임의의 양의 실수 상수이다.
좌표상의 매개변수 형태에서 곡선은,
- 와 는 실수
나선형은 임의의 점에서 접선과 반지름간의 각도 가 일정하다. 이 특성은 다음과 같이 미분 기하학 용어로 표현될 수 있다.
- 나선형 은 매개변수 에 비례 한다. 즉, 가 나선형을 특정한 나선형이게 결정하며 그리고 어느 방향으로 움직이는지를 제어하게 된다.
극단적인 경우에는 이고 나선형은 반경 의 원이 된다.
- 와 에서, 무한히 접근하는 나선형은 직선에 접근하는 성질을 갖게된다.
- 여기서 보완적인 개념의 매개변수를 피치(축경사,pitch)라고한다.
자연에 나타나는 나선형 곡선을 표현하는 로그 나선의 응용[편집]
|
로그 나선 , 축경사10° |
노틸러스 껍질의 단면,파란색점선은 성장률 매개 변수를 기반으로한다 |
스피라 미라빌리스(Spira mirabilis) 와 야콥 베르누이(Jacob Bernoulli)[편집]
스피라 미라빌리스, 직역하면 "기적 나선"에 대한 라틴어는 로그 나선의 다른 이름이기도 하다. 이 곡선은 다른 수학자들에 의해 "등각 나선형"등등으로 명명되었지만 이와 상관없이, 베르누이는 이 독특한 곡선의 특성 이름인 "나선형"의 고유한 수학적 속성에 매료되었기 때문에 특별한 표현으로 "기적"또는 "놀라운"을 수식어로 하는 놀라운 나선형(Spira mirabilis)이라는 명칭을 이 곡선에 부여했다. 이 곡선은 곡선의 연장선상에서 축경사의 크기가 증가하지만 그 모양은 각각의 연속적인 곡선, 즉 자기 유사성 (self-similarity)으로 알려진 속성만큼은 변경되지 않는다. 이 고유 한 특성의 결과로,스피라 미라빌리스는 자연에서 진화하여 노틸러스 껍질 및 해바라기 머리와 같은 고유한 특정 성장 형태로 나타난것을 확인할 수 있다. 야콥 베르누이(Jacob Bernoulli)는 "Eadem mutata resurgo"라는 문구와 함께 그의 비석에 새겨진 이러한 나선형을 원했지만 ("몇몇 변수에 의해 변형될수는 있지만 여전히 자기유사성으로 인해 수학적으로 표현되는 속성을 갖는 그러한 의미에서의 놀라운 나선형"), 실수로 아르키메데스의 나선이 대신 배치되었다고 한다.[3][4]
로그 나선과 아르키메데스의 나선[편집]
로그 나선은 기하학적 진행에서 나선의 선회 사이의 거리가 증가하는 반면에, 아르키메데스 나선에서는 이러한 거리가 일정하다는 사실에 의해 아르키메데스 나선과 구별 될 수 있다.
|
로그 나선 |
아르키메데스의 나선 |
같이 보기[편집]
각주[편집]
- ↑ (Spira mirabilis)http://jwilson.coe.uga.edu/EMT668/EMAT6680.F99/Erbas/KURSATgeometrypro/golden[깨진 링크(과거 내용 찾기)] spiral/logspiral-history.html
- ↑ Priya Hemenway (2005). 《Divine Proportion: Φ Phi in Art, Nature, and Science》. Sterling Publishing Co. ISBN 1-4027-3522-7.
- ↑ Livio, Mario (2002). 《The Golden Ratio: The Story of Phi, The World's Most Astonishing Number》. New York: Broadway Books. ISBN 0-7679-0815-5.
- ↑ Yates, R. C.: A Handbook on Curves and Their Properties, J. W. Edwards (1952), "Evolutes." p. 206