F 분포

F 분포

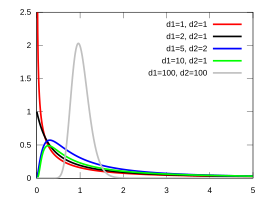
확률 밀도 함수
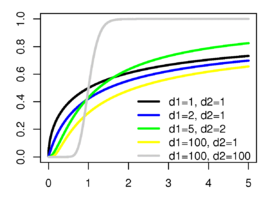
누적 분포 함수
매개변수	$d_{1}>0,\ d_{2}>0$ 자유도
지지집합	$x\in [0,+\infty )\!$
확률 밀도	${\frac {\sqrt {\frac {(d_{1}\,x)^{d_{1}}\,\,d_{2}^{d_{2}}}{(d_{1}\,x+d_{2})^{d_{1}+d_{2}}}}}{x\,\mathrm {B} \!\left({\frac {d_{1}}{2}},{\frac {d_{2}}{2}}\right)}}\!$
누적 분포	$I_{\frac {d_{1}x}{d_{1}x+d_{2}}}(d_{1}/2,d_{2}/2)\!$
기댓값	${\frac {d_{2}}{d_{2}-2}}\!$ for $d_{2}>2$
최빈값	${\frac {d_{1}-2}{d_{1}}}\;{\frac {d_{2}}{d_{2}+2}}\!$ for $d_{1}>2$
분산	${\frac {2\,d_{2}^{2}\,(d_{1}+d_{2}-2)}{d_{1}(d_{2}-2)^{2}(d_{2}-4)}}\!$ for $d_{2}>4$
비대칭도	${\frac {(2d_{1}+d_{2}-2){\sqrt {8(d_{2}-4)}}}{(d_{2}-6){\sqrt {d_{1}(d_{1}+d_{2}-2)}}}}\!$ for $d_{2}>6$
첨도	본문 참조
적률생성함수	존재하지 않음
특성함수	본문 참조

F 분포(F-distribution 또는 Snedecor's F distribution 또는 Fisher–Snedecor distribution)은 통계학에서 사용되는 연속 확률 분포로, F 검정(F test)과 분산분석(ANOVA,변량분석) 등에서 주로 사용된다.

두 확률변수 $V_{1},V_{2}$가 각각 자유도가 $k_{1},k_{2}$이고 서로 독립인 카이제곱 분포를 따른다고 할 때, 다음과 같이 정의되는 확률변수 F는 자유도가 ($k_{1},k_{2}$)인 F-분포를 따른다고 한다.

$F={\frac {V_{1}/k_{1}}{V_{2}/k_{2}}}\sim F(k_{1},k_{2})$

F분포 F(d₁, d₂)를 따르는 무작위 변수의 확률 밀도 함수는 다음과 같다.

$g(x)={\frac {1}{\mathrm {B} (d_{1}/2,d_{2}/2)}}\;\left({\frac {d_{1}\,x}{d_{1}\,x+d_{2}}}\right)^{d_{1}/2}\;\left(1-{\frac {d_{1}\,x}{d_{1}\,x+d_{2}}}\right)^{d_{2}/2}\;x^{-1}$

여기서 실수 x ≥ 0에 대해 d₁과 d₂는 양의 정수이며, B는 베타 함수이다.

누적 분포 함수는 다음과 같다.

$G(x)=I_{\frac {d_{1}x}{d_{1}x+d_{2}}}(d_{1}/2,d_{2}/2)$

여기에서 $I$는 정규화 불완전 베타 함수이다.

특성함수는 다음과 같다.

$\varphi _{\nu _{1},\nu _{2}}^{F}=M\left({\frac {\nu _{1}}{2}},-{\frac {\nu _{2}}{2}},-i{\frac {\nu _{2}}{\nu _{1}}}t\right)$

같이 보기

• 이원분산분석(2 way ANOVA)
• 회귀 분석(regression analysis)