특잇값 분해

특잇값 분해(Singular Value Decomposition, SVD)는 행렬을 특정한 구조로 분해하는 방식으로, 신호 처리와 통계학 등의 분야에서 자주 사용된다.

특잇값 분해는 행렬의 스펙트럼 이론을 임의의 직사각행렬에 대해 일반화한 것으로 볼 수 있다. 스펙트럼 이론을 이용하면 직교 정사각행렬을 고윳값을 기저로 하여 대각행렬로 분해할 수 있다.

정의

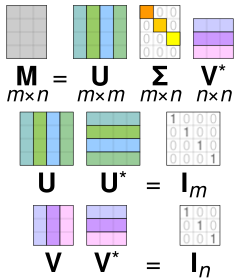특잇값 분해의 행렬곱을 시각화한 그림

실수나 복소수로 이루어진 체 K의 원소로 구성되는 m × n 행렬 M에 대해, M은 다음과 같은 세 행렬의 곱으로 분해할 수 있다.

$M=U\Sigma V^{*}\!$

여기에서 각 행렬은 다음과 같은 성질을 가진다.

• $U$는 m × m 크기를 가지는 유니터리 행렬이다.
• $\Sigma$는 m × n 크기를 가지며, 대각선상에 있는 원소의 값은 음수가 아니며 나머지 원소의 값이 모두 0인 대각행렬이다.
• $V^{*}$는 V의 켤레전치 행렬로, n × n 유니터리 행렬이다.

행렬 M을 이와 같은 세 행렬의 곱으로 나타내는 것을 M의 특잇값 분해라고 한다.

일반적으로 Σ 행렬은 더 큰 값이 먼저 나오도록, 즉 $(\Sigma )_{i,i}\geq (\Sigma )_{i+1,i+1}$이 되도록 구하며, 이렇게 할 경우 Σ는 M에 따라 유일하게 결정된다.

예제

다음과 같은 행렬 $A$가 있을 때,

$A={\begin{bmatrix}1&0&0&0&2\\0&0&3&0&0\\0&0&0&0&0\\0&4&0&0&0\end{bmatrix}}$

이 행렬을 $A=U\Sigma V^{*}$로 분해하면 다음과 같다.

$U={\begin{bmatrix}0&0&1&0\\0&1&0&0\\0&0&0&-1\\1&0&0&0\end{bmatrix}},\Sigma ={\begin{bmatrix}4&0&0&0&0\\0&3&0&0&0\\0&0&{\sqrt {5}}&0&0\\0&0&0&0&0\end{bmatrix}},V^{*}={\begin{bmatrix}0&1&0&0&0\\0&0&1&0&0\\{\sqrt {0.2}}&0&0&0&{\sqrt {0.8}}\\0&0&0&1&0\\-{\sqrt {0.8}}&0&0&0&{\sqrt {0.2}}\end{bmatrix}}$

여기에서 특잇값 분해 결과는 유일하지 않다. 예를 들어, 위의 결과에서 $V^{*}$를

$V^{*}={\begin{bmatrix}0&1&0&0&0\\0&0&1&0&0\\{\sqrt {0.2}}&0&0&0&{\sqrt {0.8}}\\{\sqrt {0.4}}&0&0&{\sqrt {0.5}}&-{\sqrt {0.1}}\\-{\sqrt {0.4}}&0&0&{\sqrt {0.5}}&{\sqrt {0.1}}\end{bmatrix}}$

로 교체할 수도 있다.

특잇값과 특이벡터

m × n 행렬 M에 대해 다음 두 조건을 만족하는 벡터 $u\in K^{m}$과 $v\in K^{n}$이 존재할 때, 음수가 아닌 실수 σ를 특잇값이라 부른다.

$Mv=\sigma u\,,M^{*}u=\sigma v.\,\!$

또한 u와 v를 각각 좌측 특이벡터와 우측 특이벡터라 부른다.

특잇값 분해 $M=U\Sigma V^{*}\!$에서 Σ의 대각선 성분들은 M의 특잇값이 되고 U와 V의 열들은 각각의 특잇값에 해당하는 좌측 특이벡터와 우측 특이벡터가 된다. 또한 위 식으로부터 다음과 같은 사실도 알 수 있다.

• m × n 행렬 M은 최소한 한개, 최대 p = min(m, n)개의 서로 다른 특잇값을 갖는다.
• M의 좌측 특이벡터들을 포함하는, K^m의 유니터리 기저를 항상 찾을 수 있다.
• M의 우측 특이벡터들을 포함하는, Kⁿ의 유니터리 기저를 항상 찾을 수 있다.

고유값 분해와의 관계

특잇값 분해는 정사각행렬만을 분해할 수 있는 고윳값 분해보다 훨씬 일반적인 행렬을 다룰 수 있지만, 두 분해는 서로 관련되어 있다.

M이 양의 정부호인 에르미트 행렬일 때 M의 모든 고윳값은 음이 아닌 실수이다. 이때 M의 특잇값과 특이벡터는 M의 고윳값과 고유벡터와 같아진다.

$M=V\Lambda V^{*}\!$

더 일반적으로는, M의 특잇값 분해가 주어졌을 때 다음과 같은 두 식이 성립한다.

$M^{*}M=V\Sigma ^{*}U^{*}U\Sigma V^{*}=V(\Sigma ^{*}\Sigma )V^{*}\!$

$MM^{*}=U\Sigma V^{*}V\Sigma ^{*}U^{*}=U(\Sigma \Sigma ^{*})U^{*}\!$

두 식의 우변은 좌변의 고윳값 분해를 나타낸다. 즉, M의 0이 아닌 특잇값들의 제곱은 M^*M 과 MM^*의 고윳값들과 같다. 또한 U는 MM^*의 고유벡터이고 V는 M^*M의 고유벡터이다.