장미곡선

장미곡선이란 수학에서 극좌표에 그려진 사인곡선을 말한다. 극좌표 등식으로는 다음과 같은 형태로 표현될 수 있다.

$r=\cos \,k\theta$

$k$가 정수일 때는 다음과 같은 상황으로 나뉜다.

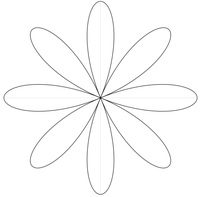
• 짝수일 때는 $2k$개의 꽃잎이 생긴다.
• 홀수일 때는 $k$개의 꽃잎이 생긴다.

$k$가 짝수일 때는 $\theta$의 값이 0에서 $2\pi$까지 변하면 전체 곡선이 그려진다. 하지만 $k$이 홀수일 때는 $\theta$의 값이 0에서 $\pi$까지 변할 때 전체 곡선이 그려진다.

$k$가 유리수일 때는 곡선은 유한의 길이에 의해 닫힌다. $k$가 무리수일 때는 닫히지 않으며 길이가 무한이다.

다음 등식에 의해(모든 $\theta$)

$\sin k\theta =\cos k\theta -{\frac {\pi }{2}}=\cos k\left(\theta -{\frac {\pi }{2k}}\right)$

곡선은 극좌표 등식이 정의한다.

$r=\sin \,k\theta$ 와 $r=\cos \,k\theta$

는 ${\frac {\pi }{2k}}\mathrm {rad}$ 바퀴를 제외하고는 동등하다.

• 
  7개의 꽃잎을 지닌 장미
  ($k=7$)
• 
  8개의 꽃잎을 지닌 장미
  ($k=4$)
• 
  $k={\frac {n}{d}}$인 $k$에 관해
  $r=\sin \,k\theta$로 정의되는 장미곡선