신장 부분 그래프

그래프 이론에서 신장 부분 그래프(身長部分graph, 영어: spanning subgraph 스패닝 서브그래프[*]) 또는 생성 부분 그래프(生成部分graph)는 모든 꼭짓점을 포함하는 부분 그래프이다.
정의[편집]
에 대하여, 만약
라면, 을 의 신장 부분 그래프라고 한다. 나무 그래프인 신장 부분 그래프를 신장 나무 부분 그래프(身長나무部分graph, 영어: spanning subtree)라고 하며, 숲 그래프인 신장 부분 그래프를 신장 숲 부분 그래프(身長숲部分graph, 영어: spanning subforest)라고 한다.
인자[편집]
신장 부분 그래프 가운데, -정규 그래프인 것을 차 인자(次因子, 영어: -factor)라고 한다. 특히, 1차 인자는 완벽 부합이라고 한다. (0차 인자는 꼭짓점 집합 위의 무변 그래프이다.)
최소 비용 신장 나무[편집]

다음이 주어졌다고 하자.
의 최소 비용 신장 나무 부분 그래프(最小費用身長部分graph, minimum cost spanning tree)는 의 연결 신장 부분 그래프 가운데, 변들의 비용의 합, 즉
를 최소화하는 것이다. (이는 항상 나무 그래프가 되며, 항상 존재한다.)
성질[편집]
임의의 그래프 및 임의의 변 집합 에 대하여, 는 신장 부분 그래프이다. 즉, 의 신장 부분 그래프의 수는 이다.
특히, 위의 무변 그래프 는 의 신장 숲 그래프이다.
모든 연결 그래프는 적어도 하나의 신장 나무 부분 그래프를 갖는다. (무한 그래프의 경우 이를 증명하려면 선택 공리가 필요하다.)
증명:
연결 그래프 의 부분 그래프 가운데 나무 그래프인 것들의 집합 를 생각하자.
이는 부분 그래프 관계에 따라 부분 순서 집합을 이룬다. 나무 그래프들의 사슬의 합집합은 항상 나무 그래프이다. (귀류법을 써 만약 아니라고 가정하면, 모든 순환은 유한 그래프이므로, 사슬의 어떤 유한한 단계에서 이러한 순환이 이미 존재해야 한다.) 즉, 는 닫힌 원순서 집합을 이룬다.
이 때문에 초른 보조정리에 따라 는 극대 원소를 갖는다. 그런데 신장 부분 그래프가 아닌 것은 극대 원소가 될 수 없다. (귀류법을 써 만약 아니라고 가정하면, 극대 원소 에 속하지 않는 꼭짓점 및 와 를 잇는 임의의 최소 경로 에 대하여, 역시 나무 그래프를 이루며, 이다.)
연결 그래프의 경우, 신장 부분 나무 그래프는 그 순환 매트로이드의 기저(극대 독립 집합)와 같다.
알고리즘[편집]
유한 연결 그래프의 최소 비용 신장 나무 부분 그래프는 프림 알고리즘이나 크러스컬 알고리즘을 사용하여 다항 시간 안에 찾을 수 있다.
예[편집]
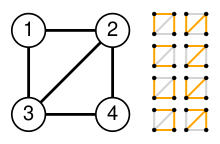
네 개의 꼭짓점을 갖는 완전 그래프 는 총 개의 신장 부분 그래프를 가지며, 그 가운데 다음 16개가 신장 나무이다.
보다 일반적으로, 케일리 공식에 따라, 의 개의 신장 부분 그래프 가운데
개가 신장 나무이다.
나무 그래프 의 신장 부분 나무 그래프는 자신 밖에 없다.
역사[편집]
최소 비용 신장 나무 부분 그래프를 구하는 문제는 1926년에 오타카르 보루프카(체코어: Otakar Borůvka, 1899~1995)가 최초로 제시하였다.[1][2][3]
참고 문헌[편집]
- ↑ Borůvka, Otakar (1926). “O jistém problému minimálním”. 《Práce moravské přírodovědecké společnosti》 (체코어) 3: 37–58. JFM 57.1343.06.
- ↑ Borůvka, Otakar (1926년 3월 5일). “Příspěvek k řešení otázky ekonomické stavby elektrovodných sítí”. 《Elektrotechnický obzor》 (체코어) 15: 153–154.
- ↑ Graham, Ronald Lewis; Hell, Pavol (1985년 1월). “On the history of the minimum spanning tree problem” (PDF). 《Institute of Electrical and Electronics Engineers Annals of the History of Computing》 (영어) 7 (1): 43–57. doi:10.1109/MAHC.1985.10011.
외부 링크[편집]
- “Factorization”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- “One-factor”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- “One-factorization”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- Weisstein, Eric Wolfgang. “Spanning tree”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- “Spanning subgraph”. 《ProofWiki》 (영어).
- “Spanning tree”. 《ProofWiki》 (영어).
- “Maximum spanning tree”. 《ProofWiki》 (영어).
- “Minimum spanning tree”. 《ProofWiki》 (영어).



























