수학 에서 모듈러 군 (영어 : modular group ) 또는 보형군 (保型群)은 정수 계수의 뫼비우스 변환 의 군 이다. 무한 이산 군 이며, 두 개의 생성원
S
{\displaystyle S}
T
{\displaystyle T}
PSL
(
2
,
Z
)
{\displaystyle \operatorname {PSL} (2,\mathbb {Z} )}
Γ
{\displaystyle \Gamma }
모듈러 군
Γ
{\displaystyle \Gamma }
표시 를 갖는 군이다.
Γ
=
⟨
S
,
T
|
S
2
=
(
S
T
)
3
=
1
⟩
{\displaystyle \Gamma =\langle {\mathsf {S}},{\mathsf {T}}|{\mathsf {S}}^{2}=({\mathsf {S}}{\mathsf {T}})^{3}=1\rangle }
즉, 이는 2차 순환군 과 3차 순환군 의 자유곱 이다.
Γ
=
Cyc
(
2
)
⋆
Cyc
(
3
)
{\displaystyle \Gamma =\operatorname {Cyc} (2)\star \operatorname {Cyc} (3)}
모듈러 군은 가산 무한 개의 원소를 가지는 군이며, 아벨 군 이 아니다. 그 중심 은 자명군 이다.
상반평면 위의 작용 [ 편집 ] 모듈러 군은 상반평면
H
=
{
τ
∈
C
:
Im
τ
>
0
}
{\displaystyle \mathbb {H} =\{\tau \in \mathbb {C} \colon \operatorname {Im} \tau >0\}}
유리 함수 로 작용 한다. 이 경우 생성원
S
{\displaystyle {\mathsf {S}}}
T
{\displaystyle {\mathsf {T}}}
S
:
z
↦
−
1
/
z
{\displaystyle {\mathsf {S}}\colon z\mapsto -1/z}
T
:
z
↦
z
+
1
{\displaystyle {\mathsf {T}}\colon z\mapsto z+1}
따라서 모듈러 군의 일반적인 원소는 다음과 같이 작용한다.
(
a
b
c
d
)
:
z
↦
a
z
+
b
c
z
+
d
{\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}\colon z\mapsto {\frac {az+b}{cz+d}}}
(
a
b
c
d
)
∈
SL
(
2
;
Z
)
{\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in \operatorname {SL} (2;\mathbb {Z} )}
이 경우 행렬
+
M
,
−
M
∈
SL
(
2
;
Z
)
{\displaystyle +M,-M\in \operatorname {SL} (2;\mathbb {Z} )}
SL
(
2
;
Z
)
/
(
−
I
)
=
PSL
(
2
;
Z
)
=
Γ
{\displaystyle \operatorname {SL} (2;\mathbb {Z} )/(-I)=\operatorname {PSL} (2;\mathbb {Z} )=\Gamma }
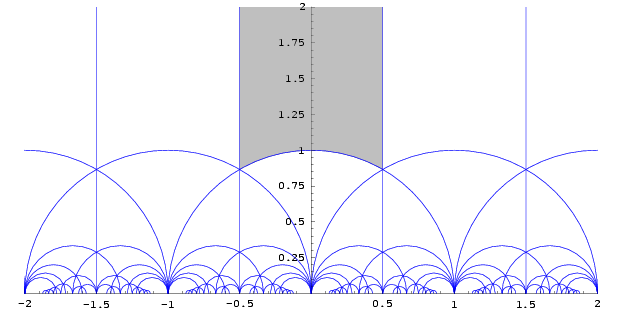
모듈러 군의 작용의 표준적인 기본 영역(영어 : fundamental domain )은 다음과 같다.
{
z
∈
H
:
|
Re
(
z
)
|
≤
1
/
2
,
|
z
|
≥
1
}
{\displaystyle \{z\in \mathbb {H} \colon |\operatorname {Re} (z)|\leq 1/2,\;|z|\geq 1\}}
보다 일반적으로, 이 작용은 리만 구 의 반구
{
τ
∈
C
:
Im
τ
≥
0
}
⊔
{
∞
}
=
H
⊔
P
R
1
{\displaystyle \{\tau \in \mathbb {C} \colon \operatorname {Im} \tau \geq 0\}\sqcup \{\infty \}=\mathbb {H} \sqcup \mathbb {P} _{\mathbb {R} }^{1}}
위로 확장될 수 있다. 이 경우, 이는 실수 사영 직선
P
R
1
=
R
⊔
{
∞
}
{\displaystyle \mathbb {P} _{\mathbb {R} }^{1}=\mathbb {R} \sqcup \{\infty \}}
대수적 수 의 집합(+∞) 또는 유리수체 (+∞)로 제한될 수 있다. 즉, 모듈러 군은 다음과 같은 부분 집합 위에 각각 작용한다.
H
{\displaystyle \mathbb {H} }
R
∖
Q
¯
{\displaystyle \mathbb {R} \setminus {\bar {\mathbb {Q} }}}
초월수 )
Q
¯
∩
R
∖
Q
{\displaystyle {\bar {\mathbb {Q} }}\cap \mathbb {R} \setminus \mathbb {Q} }
대수적 무리수 )
Q
⊔
{
∞
}
{\displaystyle \mathbb {Q} \sqcup \{\infty \}}
유리수체 위의 작용 [ 편집 ] 모듈러 군은 유리수 사영 직선
P
Q
1
=
Q
⊔
{
∞
}
{\displaystyle \mathbb {P} _{\mathbb {Q} }^{1}=\mathbb {Q} \sqcup \{\infty \}}
작용 한다. 구체적으로, 다음과 같은 집합을 생각하자.
X
=
{
(
p
,
q
)
∈
Z
2
:
gcd
{
p
,
q
}
=
1
,
p
q
≠
0
}
{\displaystyle X=\{(p,q)\in \mathbb {Z} ^{2}\colon \gcd\{p,q\}=1,\;pq\neq 0\}}
그렇다면, 그 위에
SL
(
2
;
Z
)
{\displaystyle \operatorname {SL} (2;\mathbb {Z} )}
(
a
b
c
d
)
⋅
p
q
=
a
p
+
b
q
c
p
+
d
q
(
(
a
b
c
d
)
∈
SL
(
2
;
Z
)
)
{\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}\cdot {\frac {p}{q}}={\frac {ap+bq}{cp+dq}}\qquad \left({\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in \operatorname {SL} (2;\mathbb {Z} )\right)}
이 경우, 위 행렬이 특수 선형군 에 속하므로 그 행렬식 이 1이다. 즉,
a
d
−
b
c
=
1
{\displaystyle ad-bc=1}
gcd
{
p
,
q
}
=
1
{\displaystyle \gcd\{p,q\}=1}
gcd
{
a
p
+
b
q
,
c
p
+
d
q
}
=
1
{\displaystyle \gcd\{ap+bq,cp+dq\}=1}
이게 된다. 이 작용은 추이적 작용 이다. 즉, 임의의
(
p
,
q
)
,
(
p
′
,
q
′
)
∈
X
{\displaystyle (p,q),(p',q')\in X}
M
⋅
(
p
,
q
)
=
(
p
′
,
q
′
)
{\displaystyle M\cdot (p,q)=(p',q')}
M
∈
SL
(
2
;
Z
)
{\displaystyle M\in \operatorname {SL} (2;\mathbb {Z} )}
이제, 다음과 같은 전사 함수 를 생각하자.
X
→
P
Q
1
=
Q
⊔
{
∞
}
{\displaystyle X\to \mathbb {P} _{\mathbb {Q} }^{1}=\mathbb {Q} \sqcup \{\infty \}}
(
p
,
q
)
↦
p
q
(
q
≠
0
)
{\displaystyle (p,q)\mapsto {\frac {p}{q}}\qquad (q\neq 0)}
(
±
1
,
0
)
↦
∞
{\displaystyle (\pm 1,0)\mapsto \infty }
즉,
(
p
,
q
)
{\displaystyle (p,q)}
p
/
q
{\displaystyle p/q}
p
/
q
=
(
−
p
)
/
(
−
q
)
{\displaystyle p/q=(-p)/(-q)}
SL
(
2
;
Z
)
{\displaystyle \operatorname {SL} (2;\mathbb {Z} )}
몫군
PSL
(
2
;
Z
)
{\displaystyle \operatorname {PSL} (2;\mathbb {Z} )}
유리수 사영 직선 위의 작용을 정의한다. 이 작용 역시 따라서 추이적 작용 이다.
이 작용 아래
S
{\displaystyle {\mathsf {S}}}
T
{\displaystyle {\mathsf {T}}}
S
⋅
p
q
=
−
q
p
{\displaystyle {\mathsf {S}}\cdot {\frac {p}{q}}=-{\frac {q}{p}}}
T
⋅
p
q
=
p
+
q
q
=
p
q
+
1
{\displaystyle {\mathsf {T}}\cdot {\frac {p}{q}}={\frac {p+q}{q}}={\frac {p}{q}}+1}
이 작용은 모듈러 군의, 복소수 상반평면 위의 작용을 유리수로 제한한 것이다.
꼬임군과의 관계 [ 편집 ] 모듈러 군의 보편 중심 확대 는 3차 꼬임군
Braid
(
3
)
{\displaystyle \operatorname {Braid} (3)}
Cyc
(
∞
)
↪
Braid
(
3
)
↠
PSL
(
2
;
Z
)
‖
↓
↓
Cyc
(
∞
)
↪
SL
(
2
;
R
)
¯
↠
PSL
(
2
;
R
)
{\displaystyle {\begin{matrix}\operatorname {Cyc} (\infty )&\hookrightarrow &\operatorname {Braid} (3)&\twoheadrightarrow &\operatorname {PSL} (2;\mathbb {Z} )\\\|&&\downarrow &&\downarrow \\\operatorname {Cyc} (\infty )&\hookrightarrow &{\overline {\operatorname {SL} (2;\mathbb {R} )}}&\twoheadrightarrow &\operatorname {PSL} (2;\mathbb {R} )\end{matrix}}}
여기서
SL
(
2
;
R
)
¯
{\displaystyle {\overline {\operatorname {SL} (2;\mathbb {R} )}}}
2차원 실수 특수선형군 의 범피복군 이며,
Cyc
(
∞
)
{\displaystyle \operatorname {Cyc} (\infty )}
무한 순환군 (정수의 덧셈군)이다.
합동 부분군 [ 편집 ] 모듈러 군은 합동 부분군 (영어 : congruence subgroup )이라는 일련의 부분군들을 가진다. 일반적으로, 합동 부분군 은 (아래에 정의된)
Γ
(
N
)
{\displaystyle \Gamma (N)}
Γ
{\displaystyle \Gamma }
Γ
(
N
)
⊂
G
⊂
Γ
(
1
)
{\displaystyle \Gamma (N)\subset G\subset \Gamma (1)}
N
{\displaystyle N}
G
{\displaystyle G}
준위 (영어 : level 레벨[* ] , 독일어 : Stufe 슈튜페[* ] )라고 한다.
흔히 쓰이는 합동 부분군으로는
Γ
(
N
)
{\displaystyle \Gamma (N)}
Γ
0
(
N
)
{\displaystyle \Gamma _{0}(N)}
Γ
1
(
N
)
{\displaystyle \Gamma _{1}(N)}
Γ
(
N
)
⊂
Γ
1
(
N
)
⊂
Γ
0
(
N
)
{\displaystyle \Gamma (N)\subset \Gamma _{1}(N)\subset \Gamma _{0}(N)}
모듈러 군 Γ(N ) [ 편집 ] 모듈러 군
Γ
{\displaystyle \Gamma }
주합동 부분군 (主合同部分群, 영어 : principal congruence subgroup )이라는 중요한 부분군들을 가진다.
N
≥
2
{\displaystyle N\geq 2}
N
{\displaystyle N}
동치류 들로 치환하는 다음과 같은 군 준동형 이 존재한다.
Γ
=
PSL
(
2
;
Z
)
→
PSL
(
2
;
Z
/
N
Z
)
{\displaystyle \Gamma =\operatorname {PSL} (2;\mathbb {Z} )\to \operatorname {PSL} (2;\mathbb {Z} /N\mathbb {Z} )}
이 군 준동형 의 핵 을 레벨 N 의 주합동 부분군
Γ
(
N
)
{\displaystyle \Gamma (N)}
짧은 완전열 이 있다.
1
→
Γ
(
N
)
↪
Γ
↠
PSL
(
2
;
Z
/
N
Z
)
→
1
{\displaystyle 1\to \Gamma (N)\hookrightarrow \Gamma \twoheadrightarrow \operatorname {PSL} (2;\mathbb {Z} /N\mathbb {Z} )\to 1}
구체적으로,
Γ
(
N
)
{\displaystyle \Gamma (N)}
(
a
b
c
d
)
{\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}}
에 대하여,
a
≡
d
≡
±
1
(
mod
N
)
{\displaystyle a\equiv d\equiv \pm 1{\pmod {N}}}
b
≡
c
≡
0
(
mod
N
)
{\displaystyle b\equiv c\equiv 0{\pmod {N}}}
특히,
Γ
(
2
)
=
Λ
{\displaystyle \Gamma (2)=\Lambda }
Λ 모듈러 군 (영어 : modular group Λ )라고 불린다. 이 경우
SL
(
2
;
Z
/
2
)
≅
Sym
(
3
)
{\displaystyle \operatorname {SL} (2;\mathbb {Z} /2)\cong \operatorname {Sym} (3)}
순환군 이므로 크기가 6이다. 즉,
Λ
{\displaystyle \Lambda }
지표 가 6인 부분군이다.
모듈러 군 Γ1 (N ) [ 편집 ] 모듈러 군 Γ1 (N ) 은
Γ
{\displaystyle \Gamma }
(
a
b
c
d
)
{\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}}
에 대하여,
a
≡
d
≅
1
{\displaystyle a\equiv d\cong 1}
c
≡
0
(
mod
N
)
{\displaystyle c\equiv 0{\pmod {N}}}
모듈러 군 Γ0 (N ) [ 편집 ] 모듈러 군 Γ0 (N ) 은
Γ
{\displaystyle \Gamma }
(
a
b
c
d
)
{\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}}
에 대하여,
c
≡
0
(
mod
N
)
{\displaystyle c\equiv 0{\pmod {N}}}
즉, 위와 같이
Γ
→
PSL
(
2
;
Z
/
N
Z
)
{\displaystyle \Gamma \to \operatorname {PSL} (2;\mathbb {Z} /N\mathbb {Z} )}
군 준동형 에서, 상 이 상삼각행렬 인 원소들이다.
Γ
(
N
)
{\displaystyle \Gamma (N)}
Γ
0
(
N
)
{\displaystyle \Gamma _{0}(N)}
참고 문헌 [ 편집 ] 외부 링크 [ 편집 ] 같이 보기 [ 편집 ]