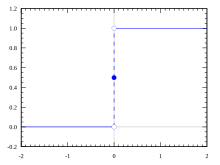
단위 계단 함수

단위 계단 함수

단위 계단 함수(unit step function) 또는 헤비사이드 계단 함수(Heaviside step function)은 0보다 작은 실수에 대해서 0, 0보다 큰 실수에 대해서 1, 0에 대해서 1/2의 값을 갖는 함수이다. 이 함수는 신호처리 분야에서 자주 사용된다.

단위 계단 함수는 디랙 델타 함수의 부정적분이다. 즉,

$H(x) = \int_{-\infty}^x { \delta(t)} \mathrm{d}t$

이 성립한다.

이산 형태

단위 계단을 이산 변수 n에 대한 함수로 나타내면

$H[n]=\begin{cases} 0, & n < 0, \\ 1, & n \ge 0, \end{cases}$

과 같이 되며 이 때 n은 정수이다. 주어진 문제가 이산적이지 않은 상황에서는 H[0]의 정의가 중요하다.

이산-시간 단위 충격량은 이산-시간 단계에서 첫 번째 차이값을 의미하는

$\delta\left[ n \right] = H[n] - H[n-1]$

으로 나타낼 수 있다. 이 함수는 크로네커 델타의 합

$H[n] = \sum_{k=-\infty}^{n} \delta[k] \,$

으로 나타낼 수 있으며 여기서

$\delta[k] = \delta_{k,0} \,$

이다.

적분 표현

때때로 복소 적분의 형태로도 나타낼 수 있다:

$H(x)=\lim_{ \epsilon \to 0^+} {i\over 2\pi}\int_{-\infty}^\infty {\mathrm{e}^{-i x \tau} \over \tau+i\epsilon} \mathrm{d}\tau =\lim_{ \epsilon \to 0^+} {1\over 2\pi i}\int_{-\infty}^\infty {\mathrm{e}^{i x \tau} \over \tau-i\epsilon} \mathrm{d}\tau.$