노턴의 정리
전기 회로에서 노턴의 정리는 두개의 단자를 지닌 전압원, 전류원, 저항의 어떠한 조합이라도 이상적인 전류원 I와 병렬저항 R로 변환하여 전기적 등가를 설명하였다. AC 시스템에서 노턴의 정리는 단순히 저항이 아닌, 일반적인 임피던스를 적용할 수 있다. 노턴 등가는 주어진 주파수에 따라 선형 전원과 임피던스의 회로망을 재분석하는데 사용된다. 회로는 이상적인 전류원과 병렬연결된 이상적인 임피던스 (리액턴스가 없는 경우 저항)로 구성된다.
노턴의 정리는 테브난의 정리를 확장한 것이다. 1926년 지멘스 할스케의 연구원 한스 페르디난트 마이어와 벨 연구소 공학자 에드워드 로리 노턴이 서로 독자적으로 발표하였다.

노턴 등가회로의 계산[편집]
등가회로를 계산하기 위해서:
- 계산된 출력전류, IAB는, 로드가 폐회로일 때 (A와 B사이의 저항이 0임을 뜻함), INo이다.
- 계산된 출력전압, VAB는, 개회로조건일 경우에 (로드저항이 없는 - 즉 저항값이 무한대임을 의미함), RNo는 VAB에 INo나눗값과 동일하다.
- 즉, 등가회로는 INo전류가 흐르는 전류원에 병렬연결된 RNo저항이다.
두 개의 방정식은 아래처럼 계산할 수 있다:
- 2a. 독립적인 전압원을 폐회로로 치환하고 독립적인 전류원은 개회로로 치환한다.
- 2b. 의존되는 전원이 없는 회로에서 RNo는 독립적인 전원을 제거한 전체저항이다.*
* 주의: 노턴 임피던스를 정하는 일반적인 방법은 1 암페어의 전류가 흐르는 회로의 출력단자에 전류원을 연결하고 단자에 인가되는 전압을 계산하는 것이다; 이 전압은 회로의 임피던스와 동일하다. 이러한 방법은 의존적인 전원을 포함하는 회로에서만 사용되어야 한다. 이러한 방법의 설명은 아래의 다이어그램에서 제외되었다.
테브난 등가 변환[편집]
테브난 등가회로로 변환하기 위해서, 아래의 방정식을 사용할 수 있다
노턴 등가회로의 예시[편집]
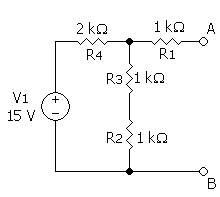 |
 |
 |

예시로, 전체전류 Itotal는 다음에 의하여 주어진다:.
로드에 흐르는 전류는, 전류 분배 법칙을 적용하여 구한다:
그리고 회로쪽으로 바라본 등가저항은 다음과 같다:
그래서 등가회로는 2 kΩ 저항과 병렬연결된 3.75 mA 전류원이다.
대중 문화[편집]
테브난의 정리와 노턴의 정리는 2006년 5월 4일과 10일에 둔즈베리 연재만화의 주제였다. [1], [2].






