국소 연결 공간
일반위상수학에서 국소 연결 공간(局所連結空間, 영어: locally connected space)은 모든 점이 연결 근방을 갖는 위상 공간이다.
정의[편집]
위상 공간 에 대하여 다음 두 조건이 서로 동치이며, 이를 만족시키는 위상 공간을 국소 연결 공간이라고 한다.
위상 공간 에 대하여 다음 두 조건이 서로 동치이며, 이를 만족시키는 위상 공간을 국소 경로 연결 공간(局所經路連結空間, 영어: locally path connected space)이라고 한다.
성질[편집]
다음과 같은 함의 관계가 존재한다.
- CW 복합체 ⊊ 국소 축약 가능 공간 ⊊ 국소 경로 연결 공간 ⊊ 국소 연결 공간
국소 경로 연결 공간 속에서 다음이 성립한다.
국소 연결 공간의 몫공간은 국소 연결 공간이다.[1]:163
(경로) 연결성과 국소 (경로) 연결성은 다음과 같은 함의 관계를 가진다.
| 경로 연결 | 연결이지만 경로 연결이 아님 | 연결이 아님 | |
|---|---|---|---|
| 국소 경로 연결 | 가능 | 불가능 | 가능 |
| 국소 연결이지만, 국소 경로 연결이 아님 | 가능 | 가능 | 가능 |
| 국소 연결이 아님 | 가능 | 가능 | 가능 |
예[편집]

(경로) 연결성과 국소 (경로) 연결성의 함의 관계에 대한 대표적인 예는 다음과 같다.
| 경로 연결 | 연결이지만 경로 연결이 아님 | |
|---|---|---|
| 국소 경로 연결 | 유클리드 공간 | (불가능) |
| 국소 연결이지만 국소 경로 연결이 아님 |
비가산 집합의 여가산 위상(영어: cocountable topology)의 뿔 | 위의 사전식 순서 위상 |
| 국소 연결이 아님 | 빗 공간 | 위상수학자의 사인 곡선 |
(연결 공간이 아닌 국소 경로 연결 공간 · 국소 연결 국소 경로 비연결 공간 · 국소 비연결 공간의 예를 얻으려면, 위 표의 예들의 분리합집합을 취하면 된다. 예를 들어, 두 개의 위상수학자의 사인 곡선의 분리합집합은 국소 연결 공간이 아닌 비연결 공간이다.)
위상수학자의 사인 곡선은 연결 공간이지만 국소 연결 공간이 아니다. (0, 1)에서 이 점을 중심으로 하는 적당히 작은 ε-구를 잡으면, (0, 1)을 포함하는 연결 성분은 열린집합이 아니기 때문이다.
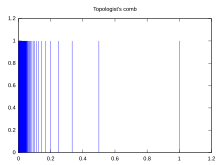
빗 공간(영어: comb space)은 의 다음과 같은 부분 공간이다.
이는 경로 연결 공간이지만 국소 연결 공간이 아니다.
유리수의 부분 공간 위상은 국소 연결 공간도, 연결 공간도 아니다.
참고 문헌[편집]
- ↑ 가 나 다 라 마 바 사 Munkres, James R. (2000). 《Topology》 (영어) 2판. Prentice Hall. ISBN 978-0-13-181629-9. MR 0464128. Zbl 0951.54001.
외부 링크[편집]
- “Locally connected space”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- “Locally path-connected space”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- Weisstein, Eric Wolfgang. “Locally connected”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- Weisstein, Eric Wolfgang. “Locally pathwise-connected”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- Weisstein, Eric Wolfgang. “Connected im Kleinen”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- “Locally path-connected space”. 《nLab》 (영어).
- “Locally connected space”. 《Topospaces》 (영어). 2016년 1월 31일에 원본 문서에서 보존된 문서. 2016년 1월 25일에 확인함.
- “Locally path-connected space”. 《Topospaces》 (영어). 2016년 1월 7일에 원본 문서에서 보존된 문서. 2016년 1월 25일에 확인함.
- “Connected not implies locally connected”. 《Topospaces》 (영어). 2016년 1월 31일에 원본 문서에서 보존된 문서. 2016년 1월 25일에 확인함.
- “Locally connected and locally path-connected spaces”. 《Mathematics and Such》. 2013년 3월 10일. 2016년 3월 4일에 원본 문서에서 보존된 문서. 2016년 1월 26일에 확인함.
- “Path-connected and locally connected space that is not locally path-connected” (영어). StackExchange. 2016년 2월 1일에 원본 문서에서 보존된 문서. 2016년 1월 26일에 확인함.







![{\displaystyle [0,1]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2fd6e9b0db782a26c033d7c728aadac9eec363a)

![{\displaystyle \{0\}\times [0,1]\cup [0,1]\times \{0\}\cup \{1/n\colon n\in \mathbb {Z} ^{+}\}\times [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0850367a33f8e67d9045f32113a760eaa642961b)